|
|
Список вопросов базы знанийМатематический анализ (курс 3)Вопрос id:744924 Укажите соответствие результатов вычисления различных степеней комплексного числа i | Левая часть | Правая часть | | | | -1 | | |
Вопрос id:744925 Укажите соответствия между заданными в первом столбце функциями и соответствующими им производными Вопрос id:744926 Указать для заданных функций их определение Вопрос id:744927 Уравнение 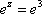 имеет ?) бесконечное множество решений 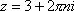 , 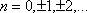 ?) решения, отличные от 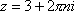 , 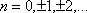 , 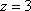 , 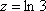 ?) единственное решение 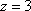 ?) единственное решение 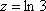 Вопрос id:744930 Аргумент, равный 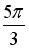 , имеют комплексные числа … Вопрос id:744931 Аргумент, равный 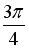 , имеют комплексные числа … Вопрос id:744932 Значение производной функции комплексного переменного 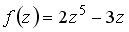 в точке 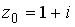 равно … Вопрос id:744933 Значение производной функции комплексного переменного 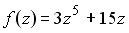 в точке 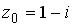 равно … Вопрос id:744934 Значение производной функции комплексного переменного 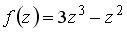 в точке 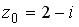 равно … ?) 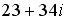 ?) - 23 ?) 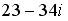 ?) 23 Вопрос id:744935 Значение производной функции комплексного переменного 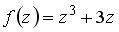 в точке 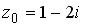 равно … ?) 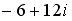 ?) 6 ?) - 6 ?) 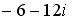 Вопрос id:744936 Модуль, равный 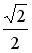 , имеют комплексные числа … Вопрос id:744937 Модуль, равный 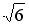 , имеют комплексные числа … Вопрос id:744938 Модуль, равный 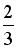 , имеют комплексные числа … Вопрос id:744939 Образом точки 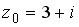 при отображении 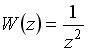 является … Вопрос id:744940 Отображение 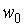 точки 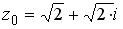 функцией 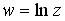 равно… Вопрос id:744941 Cинус-преобразование Фурье функции f(x) записывается в виде:
Fs(a) = 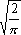 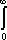 f(x)sinax dx. Найти синус-преобразование Фурье функции f(x)sinax dx. Найти синус-преобразование Фурье функции 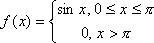 Вопрос id:744944 Общее решение одномерного волнового уравнения можно записать в виде
u(x,t) = C1(x-at) + C2(x+at), где С1 и С2 – две ?) заданные функции ?) линейно независимые функции ?) функции, определяемые в зависимости от начальных условий ?) произвольные постоянные Вопрос id:744945 Решение задачи Коши для уравнения теплопроводности Ut = a2Uxx с начальным условием
U(x,0) = j(x)=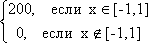 имеет вид: имеет вид: ?) U(x,t) = 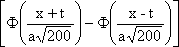 ?) U(x,t) = 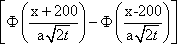 ?) U(x,t) = 200 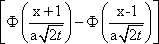 ?) U(x,t) = 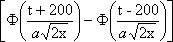 Вопрос id:744946 Решение задачи Коши для уравнения теплопроводности Ut = Uxx с начальным условием
U(x,0) = j(x)= имеет вид имеет вид ?) U(x,t) = 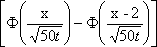 ?) U(x,t) = 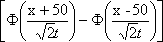 ?) U(x,t) = 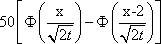 ?) U(x,t) = 50 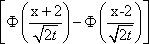 Вопрос id:744947 Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скорости 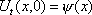 записывается в виде записывается в виде
U(x,t) = 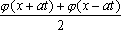 + + 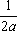 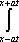 y(x)dx. y(x)dx.
Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) = х2 и начальной скорости Ut (x,0) = 0 имеет вид ?) U(x,t) = x2 +a2 t2 ?) U(x,t) = x2 + 2t2 ?) U(x,t) = 2x2 + t2 ?) U(x,t) = x2 - t2 Вопрос id:744948 Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скорости 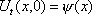 записывается в виде записывается в виде
U(x,t) = 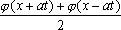 + + 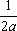 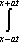 y(x)dx y(x)dx
Тогда решение уравнения Utt = Uxx при начальном отклонении U(x,0) = х3 и начальной скорости Ut (x,0) = 0 имеет вид ?) U(x,t) = x3 + xt2 ?) U(x,t) = 2x3 + 3xt2 ?) U(x,t) = x3 - 3xt2 ?) U(x,t) = x3 + 3xt2 Вопрос id:744950 Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью 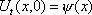 записывается в виде записывается в виде
U(x,t) = 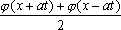 + + 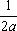 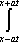 y(x)dx. y(x)dx.
Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) = sinx и начальной скорости Ut (x,0) = 0 имеет вид ?) U(x,t) = 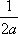 (cos(x+at) - cos(x-at)) ?) U(x,t) = 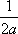 (sin(x+at) - sin(x-at)) ?) U(x,t) =  (cos(x+at) + cos(x-at)) ?) U(x,t) =  (sin(x+at) + sin(x-at)) Вопрос id:744951 Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью 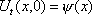 записывается в виде записывается в виде
U(x,t) = 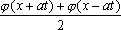 + + 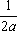 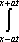 y(x)dx. y(x)dx.
Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) = cosx и начальной скорости Ut (x,0) = 0 имеет вид ?) U(x,t) = 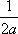 (sin(x+at) - sin(x-at)) ?) U(x,t) =  (sin(x+at) + sin(x-at)) ?) U(x,t) = 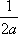 (cos(x+at) - cos(x-at)) ?) U(x,t) =  (cos(x+at) + cos(x-at)) Вопрос id:744952 Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью 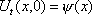 записывается в виде записывается в виде
U(x,t) = 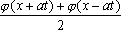 + + 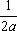 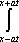 y(x)dx. y(x)dx.
Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) = e-x и начальной скорости Ut (x,0) = 0 имеет вид Вопрос id:744953 ?) U(x,t) = 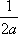 (sin(x+at) - sin(x-at)) ?) U(x,t) = 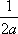 (cos(x+at) - cos(x-at)) ?) U(x,t) =  (cos(x+at) + cos(x-at)) ?) U(x,t) =  (sin(x+at) + sin(x-at)) Вопрос id:744954 ?) U(x,t) = 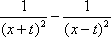 ?) U(x,t) = 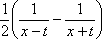 ?) U(x,t) = 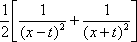 ?) U(x,t) = 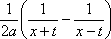 Вопрос id:744955 ?) U(x,t) = 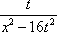 ?) U(x,t) = 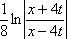 ?) U(x,t) = 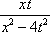 ?) U(x,t) = 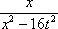 Вопрос id:744957 ?) U(x,t) = 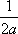 (arcsin(x+at) - arcsin(x-at)) ?) U(x,t) = 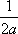 (arccos(x+at) - arccos(x-at)) ?) U(x,t) = 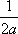 (arctg(x+at) - arctg(x-at)) Вопрос id:744958 ?) U(x,t) = 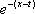 ?) U(x,t) = 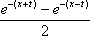 ?) U(x,t) = 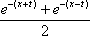 ?) U(x,t) = 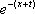 Вопрос id:744959 Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью 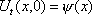 записывается в виде записывается в виде
U(x,t) = 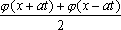 + + 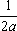 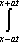 y(x)dx. y(x)dx.
Тогда решение уравнения Utt = 4Uxx при начальном отклонении U(x,0) = х2 и начальной скорости Ut (x,0) = 0 имеет вид ?) U(x,t) = 2x2 + t2 ?) U(x,t) = x2 + 2t2 ?) U(x,t) = x2 - 4t2 ?) U(x,t) = x2 + 4t2 Вопрос id:744960 Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью 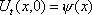 записывается в виде записывается в виде
U(x,t) = 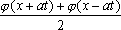 + + 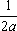 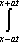 y(x)dx. y(x)dx.
Тогда решение уравнения Utt = 16Uxx при начальном отклонении U(x,0) = х2 и начальной скорости Ut (x,0) = 0 имеет вид ?) U(x,t) = x2 + 2t2 ?) U(x,t) = x2 + 16t2 ?) U(x,t) = x2 - 16t2 ?) U(x,t) = 2x2 + t2 Вопрос id:744961 ?) U(x,t) = x2 + 2t2 ?) U(x,t) = t2 ?) U(x,t) = x ?) U(x,t) = 2x2 +a2t2 Вопрос id:744962 Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью 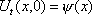 записывается в виде записывается в виде
U(x,t) = 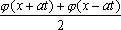 + + 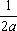 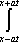 y(x)dx. y(x)dx.
Тогда решение уравнения Utt = Uxx при начальном отклонении U(x,0) = 0 и начальной скорости Ut (x,0) = х имеет вид ?) U(x,t) = x2t2 ?) U(x,t) = t2 ?) U(x,t) = x ?) U(x,t) = xt Вопрос id:744963 Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью Ut(x,0) = y(x) записывается в виде
U(x,t) = 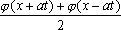 + + 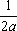 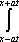 y(x)dx. y(x)dx.
Тогда решение уравнения Utt = 4Uxx при начальном отклонении U(x,0) = x и начальной скорости Ut (x,0) = х имеет вид ?) U(x,t) = x-2t ?) U(x,t) = x-8t ?) U(x,t) = x+xt ?) U(x,t) = x+2xt Вопрос id:744964 Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью Ut(x,0) = y(x) записывается в виде
U(x,t) = 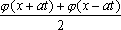 + + 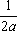 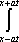 y(x)dx. y(x)dx.
Тогда решение уравнения Utt = 9Uxx при начальном отклонении U(x,0) = 0 и начальной скорости Ut (x,0) =  имеет вид имеет вид ?) U(x,t) = 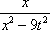 ?) U(x,t) = 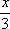 ?) U(x,t) = 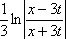 ?) U(x,t) = 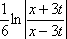 Вопрос id:744965 Уравнения характеристик для дифференциального уравнения
3ut + 4ux = 0 имеют вид ?) 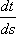 = 3; 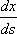 = 4 ?) 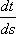 = 4; 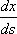 = 3 ?) 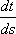 = 3; 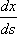 = -4 Вопрос id:744966 Выражение 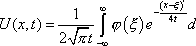 называется интегральной формулой ___для уравнения теплопроводности (ответ дать одним словом) Вопрос id:744967 Выражение 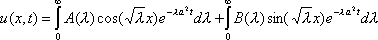 , где 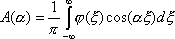 , 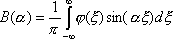 , является решением задачи Коши для уравнения ?) Лапласа ?) волнового ?) Пуассона ?) теплопроводности Вопрос id:744968 Выражение 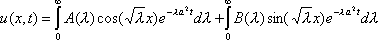 , где 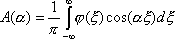 , 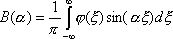 , является решением задачи Коши для уравнения___(ответ дать одним словом) Вопрос id:744969 Выражение вида 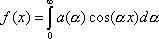 называется ?) формулой Даламбера ?) интегральной формулой Пуассона ?) интегралом Фурье по косинусам функции f(x) ?) преобразованием Фурье функции f(x) Вопрос id:744970 Выражение вида 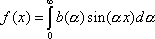 называется ?) Преобразованием Фурье функции f(x) ?) Формулой Даламбера ?) Интегральной формулой Пуассона ?) Интегралом Фурье по синусам функции f(x) Вопрос id:744971 Выражение вида f(x) = 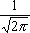 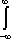 F(s)e ixsds называется ___преобразованием Фурье (ответ дать одним словом) Вопрос id:744973 Гармонические функции имеют непрерывные частные производные второго порядка и являются решением уравнения ?) волнового ?) Пуассона ?) теплопроводности ?) Лапласа Вопрос id:744974 Граница между возмущенной (колеблющейся) и не возмущенной областями среды называется ?) фронтом волны ?) стоячей волной ?) волной импульса ?) волной отклонения Вопрос id:744975 Граница между возмущенной (колеблющейся) и невозмущенной областями среды называется ___ волны (ответ дать одним словом) |














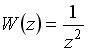 является …
является …
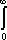 f(x)sinax dx. Найти синус-преобразование Фурье функции
f(x)sinax dx. Найти синус-преобразование Фурье функции  f(x)sinax dx. Найти синус-преобразование Фурье функции
f(x)sinax dx. Найти синус-преобразование Фурье функции  если известно, что
если известно, что  (4х-1)sinax dx = -
(4х-1)sinax dx = -  cosax dx
cosax dx f(x)cosax dx. Найти косинус-преобразование Фурье функции
f(x)cosax dx. Найти косинус-преобразование Фурье функции  если известно, что
если известно, что  (2х-3)cosax dx = -
(2х-3)cosax dx = -  sinax dx
sinax dx



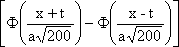
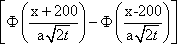
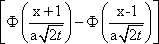
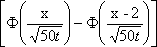
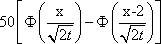
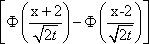
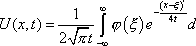 называется интегральной формулой ___для уравнения теплопроводности (ответ дать одним словом)
называется интегральной формулой ___для уравнения теплопроводности (ответ дать одним словом)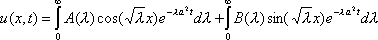 , где
, где 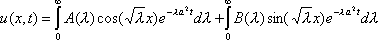 , где
, где