Список вопросов базы знанийЕГЭ Математика профильный
Вопрос id:434481 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434482 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434483 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434484 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434485 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434486 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434487 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434488 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434489 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434490 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434491 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434492 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434493 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434494 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434495 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434496 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434497 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434498 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434499 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434500 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434501 Тема/шкала: 03- Планиметрия: вычисление длин и площадей-Координатная плоскость
Вопрос id:434502 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос. Вопрос id:434503 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. Вопрос id:434504 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. Вопрос id:434505 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. Вопрос id:434506 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Вопрос id:434507 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. Вопрос id:434508 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. Вопрос id:434509 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции. Вопрос id:434510 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции? Вопрос id:434511 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса? Вопрос id:434512 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России. Вопрос id:434513 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? Вопрос id:434514 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике. Вопрос id:434515 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам. Вопрос id:434516 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и 9 прыгунов из Парагвая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что шестым будет выступать прыгун из Парагвая. Вопрос id:434517 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя. Вопрос id:434518 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе? Вопрос id:434519 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной? Вопрос id:434520 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три? Вопрос id:434521 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село в магазин за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин? Вопрос id:434522 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза. Вопрос id:434523 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»? Вопрос id:434524 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что в первый раз выпадает орёл, а во второй — решка. Вопрос id:434525 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых. Вопрос id:434526 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных. Вопрос id:434527 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест. Вопрос id:434528 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории. Вопрос id:434529 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В классе 26 человек, среди них два близнеца — Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе. Вопрос id:434530 Тема/шкала: 04-Начала теории вероятностей-Классическое определение вероятности В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрные с жёлтыми надписями на бортах, остальные — жёлтые с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями. |
 Точки O(0; 0), A(10; 8), B(8; 2) и C являются вершинами параллелограмма. Найдите ординату точки
Точки O(0; 0), A(10; 8), B(8; 2) и C являются вершинами параллелограмма. Найдите ординату точки  .
. Точки O(0; 0), B(8; 2), C(2; 6) и A являются вершинами параллелограмма. Найдите абсциссу точки A.
Точки O(0; 0), B(8; 2), C(2; 6) и A являются вершинами параллелограмма. Найдите абсциссу точки A. Точки O(0; 0), B(8; 2), C(2; 6) и A являются вершинами параллелограмма. Найдите ординату точки A.
Точки O(0; 0), B(8; 2), C(2; 6) и A являются вершинами параллелограмма. Найдите ординату точки A. Точки O(0; 0), A(10; 8), B(8; 2), C(2; 6) являются вершинами четырехугольника. Найдите абсциссу точки P пересечения его диагоналей.
Точки O(0; 0), A(10; 8), B(8; 2), C(2; 6) являются вершинами четырехугольника. Найдите абсциссу точки P пересечения его диагоналей. Точки O(0; 0), A(10; 8), B(8; 2), C(2; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
Точки O(0; 0), A(10; 8), B(8; 2), C(2; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей. Точки O(0; 0), A(6; 8), B(8; 2) являются вершинами треугольника. Найдите длину его средней линии CD, параллельной OA.
Точки O(0; 0), A(6; 8), B(8; 2) являются вершинами треугольника. Найдите длину его средней линии CD, параллельной OA. Точки O(0; 0), A(10; 0), B(8; 6), C(2; 6) являются вершинами трапеции. Найдите длину ее средней линии DE.
Точки O(0; 0), A(10; 0), B(8; 6), C(2; 6) являются вершинами трапеции. Найдите длину ее средней линии DE. Найдите абсциссу точки пересечения прямой, заданной уравнением 3x + 2y = 6, с осью Ox.
Найдите абсциссу точки пересечения прямой, заданной уравнением 3x + 2y = 6, с осью Ox. Найдите ординату точки пересечения прямой, заданной уравнением 3x + 2y = 6, с осью Oy.
Найдите ординату точки пересечения прямой, заданной уравнением 3x + 2y = 6, с осью Oy. Найдите абсциссу точки пересечения прямых, заданных уравнениями 3x + 2y = 6 и y = x.
Найдите абсциссу точки пересечения прямых, заданных уравнениями 3x + 2y = 6 и y = x. Найдите ординату точки пересечения прямых, заданных уравнениями 3x + 2y = 6 и y = −x.
Найдите ординату точки пересечения прямых, заданных уравнениями 3x + 2y = 6 и y = −x. Найдите угловой коэффициент прямой, заданной уравнением 3x + 4y = 6.
Найдите угловой коэффициент прямой, заданной уравнением 3x + 4y = 6. Окружность с центром в начале координат проходит через точку P(8; 6). Найдите ее радиус.
Окружность с центром в начале координат проходит через точку P(8; 6). Найдите ее радиус. Какого радиуса должна быть окружность с центром в точке P(8; 6), чтобы она касалась оси абсцисс?
Какого радиуса должна быть окружность с центром в точке P(8; 6), чтобы она касалась оси абсцисс? Какого радиуса должна быть окружность с центром в точке P (8; 6), чтобы она касалась оси ординат?
Какого радиуса должна быть окружность с центром в точке P (8; 6), чтобы она касалась оси ординат?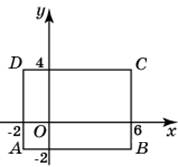 Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4). Найдите абсциссу центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Найдите абсциссу центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4). Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).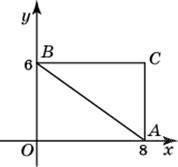 Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).
Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6). Найдите абсциссу центра окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).
Найдите абсциссу центра окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6). Найдите ординату центра окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).
Найдите ординату центра окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).