Список вопросов базы знанийВычислительная математика (курс 1)Вопрос id:736003 Функция u(x,y) задана таблицей.
Значение частной производной ?) 3 ?) 2,4 ?) 1,987 ?) 1,5 Вопрос id:736004 Функция u(x,y) задана таблицей
значение частной производной ?) 8,8 ?) 10 ?) 20 ?) 5 Вопрос id:736005 Функция u(x,y) задана таблицей
Значение оператора Лапласа ?) 0,75 ?) 10 ?) 20 ?) 0 Вопрос id:736006 Функция u(x,y) задана таблицей
Значение частной производной ?) 2 ?) 2,6 ?) 1,8 ?) 1,4 Вопрос id:736007 Функция u(x,y) задана таблицей
Значение частной производной ?) 10 ?) 11,8 ?) 12 ?) 9 Вопрос id:736008 Функция u(x,y) задана таблицей
Значение частной производной ?) 2,56 ?) 10 ?) 9 ?) 11 Вопрос id:736009 Функция u(x,y) задана таблицей
значение частной производной ?) 4 ?) 2,5 ?) 3 ?) 2 Вопрос id:736010 Функция u(x,y) задана таблицей
значение частной производной ?) 3 ?) 2 ?) 4 ?) 3,6 Вопрос id:736011 Функция u(x,y) задана таблицей
значение частной производной ?) 2,5 ?) 2 ?) 1 ?) 5 Вопрос id:736012 Функция u(x,y) задана таблицей
значение частной производной ?) 5 ?) 10 ?) 2,6 ?) 4 Вопрос id:736014 Функция u(x,y) задана таблицей
значение частной производной ?) 3 ?) 1 ?) 2 ?) 6 Вопрос id:736015 Функция u(x,y) задана таблицей
Значение оператора ?) 10 ?) 20 ?) 0 ?) 0,5 Вопрос id:736016 Функция u(x,y) задана таблицей
Значение величины ?) -0,5 ?) 3,5 ?) 0,5 ?) 1,5 Вопрос id:736017 Функция u(x,y) задана таблицей
Значение частной производной ?) 2 ?) 1,5 ?) 3 ?) 10 Вопрос id:736018 Функция u(x,y) задана таблицей
Значение величины ?) - 0,5 ?) 0,5 ?) 0 ?) 3,5 Вопрос id:736019 Функция u(x,y) задана таблицей
значение частной производной ?) 5 ?) 2 ?) 3 ?) 1 Вопрос id:736020 Функция u(x,y) задана таблицей
значение частной производной ?) 1 ?) 2 ?) 2,5 ?) 3 Вопрос id:736021 Функция u(x,y) задана таблицей
значение частной производной ?) 0,5 ?) 1,5 ?) -2 ?) 2 Вопрос id:736022 Функция u(x,y) задана таблицей
значение частной производной ?) -1 ?) 1 ?) 1,5 ?) 3 Вопрос id:736023 Функция u(x,y) задана таблицей
значение частной производной x = 0,9; y = 3,2 (точка в таблице помечена галочкой) равно ?) 3 ?) 10 ?) 1,6 ?) 5 Вопрос id:736024 Функция u(x,y) задана таблицей
значение частной производной ?) 3,8 ?) 6 ?) 2 ?) 4 Вопрос id:736025 Верны ли утверждения? А) Уравнение B) Уравнение ?) A – да, B – да ?) A – нет, B - да ?) A – да, B - нет ?) A – нет, B – нет Вопрос id:736026 Верны ли утверждения? А) Уравнение B) Уравнение ?) A – нет, B - да ?) A – да, B - нет ?) A – да, B – да ?) A – нет, B – нет Вопрос id:736027 Верны ли утверждения? А) Уравнение Лапласа имеет параболический тип B) Уравнение Лапласа имеет одну пространственную переменную ?) A – да, B – да ?) A – да, B - нет ?) A – нет, B - да ?) A – нет, B – нет Вопрос id:736028 Верны ли утверждения? А) Уравнение Лапласа описывает нестационарные процессы В) Уравнение Лапласа имеет параболический тип ?) A – да, B – да ?) A – нет, B – нет ?) A – нет, B - да ?) A – да, B - нет Вопрос id:736029 Верны ли утверждения? А) Уравнение Лапласа описывает стационарные процессы B) Уравнение Лапласа имеет гиперболический тип ?) A – нет, B - да ?) A – нет, B – нет ?) A – да, B - нет ?) A – да, B – да Вопрос id:736030 Верны ли утверждения? А) Уравнение Лапласа описывает стационарные процессы B) Уравнение Лапласа имеет в правой части нуль ?) A – да, B - нет ?) A – да, B – да ?) A – нет, B - да ?) A – нет, B – нет Вопрос id:736031 Верны ли утверждения? А) Уравнение Пуассона описывает стационарные процессы B) Уравнение Пуассона имеет ненулевую правую часть ?) A – нет, B - да ?) A – да, B - нет ?) A – да, B – да ?) A – нет, B – нет Вопрос id:736032 Верны ли утверждения? А) Уравнение Пуассона описывает стационарные процессы B) Уравнение Пуассона имеет эллиптический тип ?) A – да, B – да ?) A – нет, B - да ?) A – да, B - нет ?) A – нет, B – нет Вопрос id:736033 Для интегральных уравнений А) однородное уравнение Фредгольма второго рода всегда имеет нулевое решение B) ненулевые решения ?) A – да, B - нет ?) A – нет, B - да ?) A – нет, B – нет ?) A – да, B – да Вопрос id:736034 Для интегральных уравнений А) Ядро B) Ядро ?) A – да, B – да ?) A – нет, B – нет ?) A – нет, B – да ?) A – да, B - нет Вопрос id:736035 Для интегральных уравнений А) Ядро B) Ядро ?) A – нет, B – да ?) A – да, B – да ?) A – да, B - нет ?) A – нет, B – нет Вопрос id:736036 Для интегральных уравнений Фредгольма второго рода A) ненулевые решения однородного уравнения называют собственными функциями B) значения величины ?) A – да, B - нет ?) A – нет, B – нет ?) A – нет, B - да ?) A – да, B – да Вопрос id:736037 Для интегральных уравнений Фредгольма второго рода A) однородное уравнения всегда имеет нулевое решение B) ненулевое решение существует при любом значении величины ?) A – нет, B – нет ?) A – да, B - нет ?) A – нет, B - да ?) A – да, B – да Вопрос id:736038 Для интегральных уравнений Фредгольма справедливы ли следующие утверждения? А) все собственные значения симметричного ядра – действительные числа B) собственные функции симметричного ядра ортогональны ?) A – да, B – да ?) A – да, B - нет ?) A – нет, B – да ?) A – нет, B – нет Вопрос id:736039 Для интегральных уравнений Фредгольма справедливы ли следующие утверждения? А) симетричное ядро имеет хотя бы одно собственное значение B) собственные функции симметричного ядра не могут быть ортогональны ?) A – да, B – да ?) A – нет, B – да ?) A – да, B - нет ?) A – нет, B – нет Вопрос id:736040 Для интегральных уравнений A) ненулевые решения B) ненулевые решения ?) A – да, B – да ?) A – нет, B – нет ?) A – да, B - нет ?) A – нет, B - да Вопрос id:736041 Для уравнений в частных производных могут быть использованы следующие численные методы решения: А) вариационные В) конечно-разностные ?) A – нет, B - да ?) A – да, B – да ?) A – да, B - нет ?) A – нет, B – нет Вопрос id:736042 Для уравнений в частных производных могут быть использованы следующие численные методы решения: А) метод Симпсона В) метод Гаусса ?) A – нет, B – нет ?) A – да, B - нет ?) A – нет, B - да ?) A – да, B – да Вопрос id:736043 Для уравнений в частных производных могут быть использованы следующие численные методы решения: А) прямые В) одношаговые ?) A – да, B – да ?) A – да, B - нет ?) A – нет, B – нет ?) A – нет, B - да Вопрос id:736044 Задача решения дифференциального уравнения с дополнительными условиями называется ?) задачей Неймана ?) краевой задачей ?) задачей Коши ?) задачей Дирихле Вопрос id:736045 Задача решения дифференциального уравнения с дополнительными условиями
называется ?) задачей Неймана ?) краевой задачей ?) задачей Коши ?) задачей Дирихле Вопрос id:736046 Неустойчивость разностной схемы может быть А) условной В) безусловной ?) A – нет, B – нет ?) A – да, B – да ?) A – нет, B - да ?) A – да, B - нет Вопрос id:736047 Постановка задачи для уравнения в частных производных включает в себя: A) условия неединственности решения задачи В) область решения задачи ?) A – нет, B – нет ?) A – да, B - нет ?) A – да, B – да ?) A – нет, B - да Вопрос id:736048 Постановка задачи для уравнения в частных производных включает в себя: А) вид уравнения В) дополнительные условия, обеспечивающие единственность решения задачи ?) A – да, B – да ?) A – нет, B - да ?) A – нет, B – нет ?) A – да, B - нет Вопрос id:736049 Постановка задачи для уравнения в частных производных включает в себя А) вид уравнения В) область решения задачи ?) A – нет, B - да ?) A – нет, B – нет ?) A – да, B - нет ?) A – да, B – да Вопрос id:736050 Система линейных уравнений для разностной схемы с использованием центральных разностей для задачи является ?) трехдиагональной ?) диагональной ?) двухдиагональной ?) пятидиагональной Вопрос id:736051 Существуют следующие методы решения интегральных уравнений: А) метод последовательных приближений В) квадратурные методы ?) A – нет, B - да ?) A – да, B - нет ?) A – да, B – да ?) A – нет, B – нет Вопрос id:736052 Тип уравнения в частных производных второго порядка ?) коэффициентами при первых производных ?) правой частью уравнения ?) величиной коэффициентов при вторых производных ?) знаками величин Вопрос id:736053 Уравнение в частных производных А) имеет второй порядок В) является линейным для любых функций, задающих коэффициенты уравнения ?) A – нет, B - да ?) A – нет, B – нет ?) A – да, B – нет ?) A – да, B – да |



 , вычисленное с помощью центральных разностей в точке x = 0,9; y = 2,2 равно
, вычисленное с помощью центральных разностей в точке x = 0,9; y = 2,2 равно








 , вычисленное с помощью центральных разностей в точке x = 0,9; y = 2,2 равно
, вычисленное с помощью центральных разностей в точке x = 0,9; y = 2,2 равно
 , вычисленное с помощью центральных разностей в точке x = 0,9; y = 2,2 равно
, вычисленное с помощью центральных разностей в точке x = 0,9; y = 2,2 равно

 , вычисленное с помощью центральных разностей, в точке x = 0,9; y = 2,2 равно
, вычисленное с помощью центральных разностей, в точке x = 0,9; y = 2,2 равно





 называется волновым уравнением
называется волновым уравнением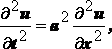 имеет гиперболический тип
имеет гиперболический тип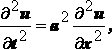 описывает стационарные процессы
описывает стационарные процессы имеет гиперболический тип
имеет гиперболический тип определяется следующим:
определяется следующим: