|
|
Список вопросов базы знанийМатематика (курс 13)Вопрос id:739427 Статистика F, использующаяся в процедуре проверки равенства дисперсий двух генераль-ных совокупностей, имеет распределение ?) χ2 ?) Стьюдента ?) N(0,1) ?) Фишера-Снедекора Вопрос id:739428 Студент опаздывает на занятия в 4-х случаях из 7. Найти вероятность того, что за 6 учебных дней студент | Левая часть | Правая часть | опоздает ровно два раза | | ни разу не опоздает | | опоздает один или два раза | | опоздает ровно 3 раза | |
Вопрос id:739429 Сумма 2 двоичных чисел (10010111 и 10101000) в десятичном формате равна Вопрос id:739430 У матрицы  ?) определитель равен -2 ?) определитель равен 0 ?) имеются зависимые строки ?) все строки независимы Вопрос id:739431 У матрицы 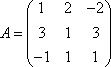 ?) определитель равен -22 ?) имеются зависимые строки ?) определитель равен 0 ?) все строки независимы Вопрос id:739432 Укажите верные соответствия между многочленами и их координатами в базисе 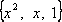 | Левая часть | Правая часть | | (1, –1,2) | | (2,1, –1)) | | (2, –1,1) |
Вопрос id:739433 Укажите соответствие между видом функции и ее названием | Левая часть | Правая часть | | показательная | | тригонометрическая | | парабола (многочлен) |
Вопрос id:739434 Укажите соответствие между названиями теорем (левая колонка) и их формулировками (правая колонка) | Левая часть | Правая часть | Теорема Лагранжа | пусть 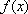 задана на 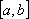 и удовлетворяет двум условиям: 1) 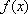 непрерывна на 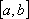 ; 2) 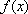 имеет производную 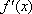 в 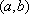 . Тогда внутри 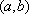 найдется по крайней мере одна такая точка с, что 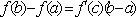 | Теорема Ролля | пусть  задана на промежутке 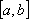 и удовлетворяет на этом промежутке следующим условиям: 1)  непрерывна на 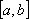 ; 2) 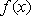 имеет производную во всех точках  ; 3)  . Тогда внутри 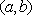 найдется хотя бы одна такая точка  , что 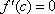 | Теорема Ферма | если функция 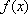 , определенная в интервале  , достигает в некоторой внутренней точке  этого интервала наибольшее или наименьшее значение и существует производная 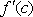 , то  |
Вопрос id:739435 Укажите соответствие между терминами (левая колонка) и их определениями (правая колонка) | Левая часть | Правая часть | разность множеств А и В | множество (С) всех элементов, принадлежащих хотя бы одному из множеств А и В:C =  | объединение множеств А и В | множество (С) всех элементов, принадлежащих обоим множествам А и В: C = 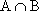 | пересечение множеств А и В | множество (С), состоящее из тех элементов множества А, которые не принадлежат множеству В:C = A\B |
Вопрос id:739436 Укажите соответствие между терминами (левая колонка) и их определениями (правая колонка) | Левая часть | Правая часть | Убывающая в ин- тервале 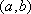 функция | функция, для которой на заданном интервале определения  существует постоянное k > 0, такое, что | f( x)| ≤ k | Возрастающая в ин-тервале 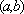 функция | функция, для которой при любых х1,х2 ⊂ (а, b) таких, что х1 < х2, выполняется неравенство f(x1) > f(x2) | Ограниченная на ин-тервале 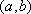 функция | функция, для которой при любых х1,х2 ⊂ (а, b) таких, что х1 < х2, выполняется неравенство f(x1) < f(x2) |
Вопрос id:739437 Укажите соответствие между терминами (левая колонка) и их определениями (правая колонка) | Левая часть | Правая часть | Два замечательных предела | производная равна tg α, где α - угол, который образует касательная к кривой, проведенная в точке, где берется производная | Геометрический смысл производной | | Производная функции в точке х0 | предел отношения приращения функции D y к приращению аргумента D х при стремлении D х к нулю: 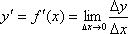 |
Вопрос id:739438 Укажите соответствие между терминами (левая колонка) и их определениями (правая колонка). Для дискретной случайной величины справедливы следующие определения | Левая часть | Правая часть | среднеквадратичное отклонение | | дисперсия | | математическое ожидание | |
Вопрос id:739439 Укажите соответствие между терминами (левая колонка) и их определениями (правая колонка). Для непрерывной случайной величины справедливы следующие определения | Левая часть | Правая часть | среднеквадратичное отклонение | | математическое ожидание | | дисперсия | |
Вопрос id:739440 Укажите соответствие между терминами (левая колонка) и соответствующими определениями (правая колонка) | Левая часть | Правая часть | Область значений функции двух переменных 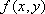 | | Линия уровня функции 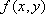 | множество 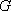 пар значений переменных  и  , для которых существует функция 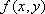 | Область существования функции двух переменных  | множество всех значений, принимаемых функцией 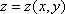 в области определения |
Вопрос id:739441 Укажите соответствие между терминами (левая колонка) и соответствующими формулами (правая колонка) | Левая часть | Правая часть | Повторный интеграл от функции f(x, y) по правильной в направлении оси Oy области D | | Аддитивность двойного интеграла | 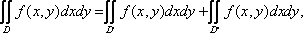 если D' и D''- подобласти области D: D = ( D'  D D'') | Двойной интеграл | | Линейность двойного интеграла | |
Вопрос id:739442 Укажите соответствие между терминами (левая колонка) и соответствующими формулами (правая колонка) | Левая часть | Правая часть | Формула Остроград-ского-Гаусса | | Формула Грина | | Формула Стокса | |
Вопрос id:739443 Укажите соответствие между терминами (левая колонка) и соответствующими формулами и определениями (правая колонка) | Левая часть | Правая часть | Линейность неопре-деленного интеграла | | Интегральная сумма функции 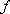 в проме-жутке [ а, b] | если функция  непрерывна, то она имеет первообразную | Условие интегрируе-мости функции 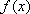 | |
Вопрос id:739444 Укажите соответствие между терминами (левая колонка) и соответствующими формулами и определениями (правая колонка) | Левая часть | Правая часть | Формула Ньютона-Лейб-ница | | Площадь криволинейной трапеции, ограниченной осью ОХ, кривой  , прямыми  и  | | Формула интегрирования по частям | |
Вопрос id:739445 Укажите соответствие между терминами (левая колонка) и соответствующими формулами и определениями (правая колонка) | Левая часть | Правая часть | Абсолютная сходимость  | если расходится интеграл 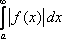 и сходится интеграл 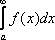 | Несобственный интеграл первого рода | интеграл с бесконечными пределами интегрирования 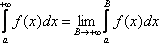 | Условная сходимость 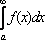 | если сходится интеграл 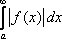 | Несобственный интеграл второго рода | интеграл от неограниченной функции на промежутке интегрирования, если функция непрерывна в точке b:  |
Вопрос id:739446 Укажите соответствие между терминами (левая колонка) и соответствующими формулами и определениями (правая колонка) | Левая часть | Правая часть | Частная производная для функции 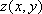 по переменной  | | Условие непрерывности 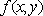 в точке  | | Частная производная для функции 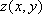 по переменной  | |
Вопрос id:739447 Укажите соответствие между терминами (левая колонка) и соответствующими формулами и определениями (правая колонка) | Левая часть | Правая часть | Полный дифференциал  | линейная часть приращения 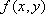 - 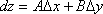 | Достаточное условие дифференцируемости 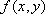 в точке  | существование частных производных 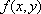 в этой точке | Необходимое условие дифференцируемости  в точке 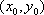 | непрерывность частных производных 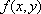 в этой точке |
Вопрос id:739448 Укажите соответствие между терминами (левая колонка) и соответствующими формулами и определениями (правая колонка) | Левая часть | Правая часть | Функция 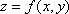 имеет в точке 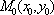 максимум (минимум) | | Необходимые усло-вия существования экстремума для функции 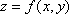 в точке  | | Производная сложной функции | существует такая окрестность точки 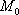 , что для всех точек  из этой окрестности, отличных от 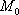 выполняется неравенство 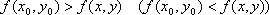 |
Вопрос id:739449 Укажите соответствие между терминами (левая колонка) и соответствующими формулами и определениями (правая колонка) | Левая часть | Правая часть | Эластичность производства | учитывая структуру цен, доход и собственные предпочтения, потребитель приобретает определенное количество благ на определенную сумму I. | Модель потребительского выбора | | Эластичность выпуска по i-му ресурсу | сумма эластичностей выпуска по всем ресурсам. |
Вопрос id:739450 Укажите соответствие между терминами (левая колонка) и соответствующими формулами и определениями (правая колонка) | Левая часть | Правая часть | Сферические координаты точки P(r,φ,ψ) | тройка чисел  , где  - полярные координаты проекции точки на плоскость Oxy, а z - обычная декартова координата точки P вдоль оси z | Полярные координаты точки P(ρ, φ) | пара  , где 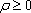 - расстояние от точки до полюса, а 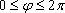 - угол, который образует с полярной осью радиус-вектор точки | Цилиндрические координаты точки P(ρ, φ, z) | тройка чисел 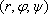 , где r - радиус-вектор точки P, φ - полярная координата проекции точки на плоскость Oxy, а 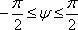 - угол, образованный радиус-вектором точки r и координатной плоскостью Oxy |
Вопрос id:739451 Укажите соответствие между терминами (левая колонка) и соответствующими формулами и определениями (правая колонка) | Левая часть | Правая часть | Циркуляция векторного поля 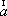 (скаляр) | | Поток векторного поля 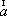 через поверхность  (скаляр) |  , где 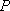 , 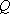 , 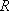 - проекции вектора  | Вихрь (ротор) век- торного поля 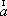 (вектор) | | Дивергенция векторного поля  (скаляр) | 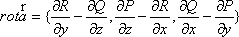 , где  ,  , 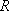 - проекции вектора 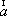 |
Вопрос id:739452 Уравнение  является характеристическим для однородных дифференциальных уравнений, соответствующих нижеприведенным неоднородным Вопрос id:739453 Уравнение  является характеристическим для однородных дифференциальных уравнений, соответствующих нижеприведенным неоднородным Вопрос id:739454 Уравнение вида 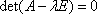 относительно 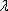 называется ___ уравнением матрицы АВопрос id:739455 Уравнение регрессии Y на Х, выраженное через коэффициент корреляции r, имеет вид Вопрос id:739456 Установить соответствие между векторами 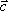 в столбцах ниже | Левая часть | Правая часть | даны два вектора 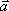 (1, -2, 3) и  (2, 1, 4), вектор 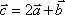 будет |  (4,-3,10) | даны два вектора 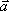 (0, -2, 3) и 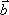 (1, 1, 4), вектор 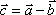 будет | 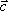 (-3,-4,3) | даны два вектора  (1, -2, 3) и 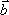 (2, 1, 0), вектор 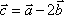 будет | 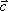 (-1,-3,-1) | даны два вектора 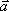 (3, -2, 3) и 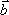 (0, 1, 2), вектор 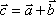 будет | 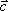 (3,-1,5) |
Вопрос id:739457 Установить соответствие между матрицами в левом столбце и их определителями в правом столбце | Левая часть | Правая часть | | det A = 3 | | det A = 5 | | det A = -7 | | det A = -21 |
Вопрос id:739458 Установить соответствие между матрицами в левом столбце и обратными матрицами в правом столбце Вопрос id:739459 Установить соответствие между матрицами в левом столбце и транспонированными матрицами в правом столбце Вопрос id:739460 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | множество всех чисел х, которые удовлетворяют неравенствам a≤ х ≤b. | ε- окрестность точки х0. (х0 - ε, х0 +ε) | интервал, в котором хотя бы один конец уходит в бесконечность | открытый интервал (a,b) | любой открытый интервал, содержащий точку х0. | бесконечный интервал | множество всех чисел х, которые удовлетворяют неравенствам a< х <b. | закрытый интервал [a,b] |
Вопрос id:739461 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | второй замечательный предел | | предел функции при  | | первый замечательный предел | |
Вопрос id:739462 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | если обратная х величина  (ее предел = 0 ), то х называется | бесконечно большой величиной (б.б.) | предел функции при 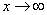 | | если величина х стремится к 0 (  ), то она называется | бесконечно малой величиной (б.м.) |
Вопрос id:739463 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | | 2/3 | | 1/2 | | - 4 |
Вопрос id:739464 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | умножение вектора на число подчиняется сочетательному закону | λ(μ 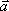 ) = (λμ) 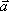 | сумма векторов подчиняется переместительному закону | | деление вектора на число λ ≠ 0 эквивалентно умножению вектора на число 1/ λ | | сумма двух противоположных векторов равна 0-вектору | 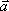 / λ = (1/ λ)· 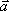 |
Вопрос id:739465 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | Уравнение прямой в общем виде | | Уравнение прямой с угловым коэффициентом | | Уравнение прямой в отрезках | | Уравнение прямой, проходящей через заданную точку М1и имеющую определенный угловой коэффициент k | | Уравнение прямой, проходящей через 2 заданные точки М1 и М2 | |
Вопрос id:739466 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | Условие перпендикулярности 2-х прямых | k1 =k2 | Условие параллельности 2-х прямых | | Формула для вычисления угла между 2-х прямыми | |
Вопрос id:739467 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | каноническое уравнение параболы | | каноническое уравнение эллипса | | каноническое уравнение гиперболы | | каноническое уравнение окружности | |
Вопрос id:739468 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | в каноническое уравнение окружности, как параметры, входят | координаты центра и величины полуосей | в каноническое уравнение эллипса, как параметры, входят | координаты центра и величины ее полуосей | для того, чтобы записать уравнения асимптот гиперболы, надо знать | координаты центра и радиус |
Вопрос id:739469 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | число векторов базиса, равное n | координаты вектора в этом базисе | максимальное число линейно независимых векторов | ранг системы векторов | коэффициенты в разложении вектора по данному базису | размерность пространства  |
Вопрос id:739470 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | | неоднородная совместимая система | | неоднородная несовместимая система | | однородная система |
Вопрос id:739471 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | собственным базисом матрицы  могут служить векторы | | вектор  является собственным для матрицы 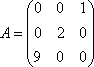 , отвечающим собственному значению | 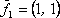 , 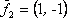 | вектор 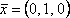 является собственным для матрицы  , отвечающим собственному значению, равному | | собственный базис матрицы 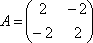 может состоять из векторов | 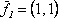 , 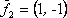 |
Вопрос id:739472 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | собственный базис матрицы 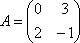 может состоять из векторов | | вектор 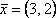 является собственным для матрицы 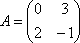 , отвечающим собственному значению | | для матрицы 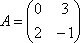 собственным является вектор | 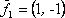 , 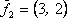 | вектор 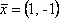 является собственным для матрицы 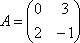 , отвечающим собственному значению | |
Вопрос id:739473 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | собственный базис матрицы 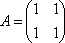 может состоять из векторов | | собственный базис матрицы 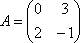 может состоять из векторов |  , 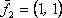 | вектор  является собственным для матрицы 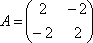 и отвечает собственному значению | | вектор 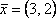 является собственным для матрицы 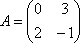 , отвечающим собственному значению | 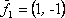 , 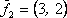 |
Вопрос id:739474 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | суперпозиция функций | операция φ, обладающая переместительным свойством: aj b = bj a | формула | операция φ, обладающая сочетательным свойством 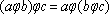 | коммутативная бинарная операция | функция, полученная из n-местной функции f(x1, x2, ..., xn) и системы n функций g1, g2, ..., gn некоторой подстановкой функций g1, g2, ..., gn во внешнюю функцию f вместо переменных и переименованиями переменных | ассоциативная бинарная операция | выражение, описывающее суперпозицию и содержащее функциональные знаки, символы независимых переменных (аргументов) и констант |
Вопрос id:739475 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | антисимметричное отношение | бинарное отношение, обладающее свойством: для любого а выполнено а R a | антирефлексивное отношение | бинарное отношение - такое, что для любых  и  выполнено: если a ≠ b, то aRb Þ  (т.е. если a и b - в этом порядке(!) - находятся в отношении R, то b и a - нет). Это же свойство выражают иначе: если aRb и bRa, то a = b | транзитивное отношение | бинарное отношение, обладающее свойством: для любых a, b выполнено aRb Þ bRa (т.е. из aRb следует bRa) | симметричное отношение | бинарное отношение, обладающее свойством: для любого а выполнено а a a | рефлексивное отношение | бинарное отношение, обладающее свойством: для любых трех элементов a, b, c выполнено: если aRb и bRc, то aRc . |
Вопрос id:739476 Установить соответствие между строками в столбцах ниже | Левая часть | Правая часть | префиксный код | кодирование множества объектов словами в двоичном алфавите В = {0, 1} | разделимый код | код V={v1, v2,…,vn}, допускающий единственность декодирования при использовании без разделителей | двоичное кодирование | код V={v1, v2,…,vn}, если никакое кодовое слово vk не является началом никакого другого слова 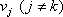 | алфавитное кодирование | кодирование множества объектов словами в некотором алфавите | равномерный код | код V={v1, v2,…,vn}, в котором все кодовые слова имеют одинаковую длину |
|

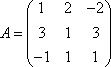



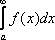
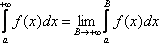



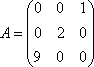 , отвечающим собственному значению
, отвечающим собственному значению , отвечающим собственному значению, равному
, отвечающим собственному значению, равному