Список вопросов базы знанийВычислительные методы (магистр. курс 1)Вопрос id:1639651 Разностная схема называется устойчивой, если малому изменению входных данных соответствует малое изменение решения ?) да ?) нет Вопрос id:1639652 Свойства решений уравнений в частных производных и особенность постановки начальных и граничных условий зависят от типа уравнений ?) да ?) нет Вопрос id:1639653 Система разностных уравнений называется системой разностных уравнений с переменными коэффициентами ?) нет ?) да Вопрос id:1639654 Системы координат используются: полярная, сферическая, цилиндрическая ?) нет ?) да Вопрос id:1639655 Смешанные задачи - нестационарные задачи, решаемые в ограниченной области, при формулировке которых ставятся и начальные, и граничные условия ?) нет ?) да Вопрос id:1639656 Уравнение называется эволюционным, если в качестве одной из независимых переменных используется время ?) нет ?) да Вопрос id:1639657 Уравнение не бывает ?) нелинейное ?) квазилинейное ?) линейное ?) криволинейное Вопрос id:1639658 Уравнение с частными производными - уравнение, в котором искомая функция зависит от нескольких переменных, и уравнения содержат частные производные искомых функций ?) нет ?) да Вопрос id:1639659 Шаблон разностной схемы показывает, какие сеточные функции входят в разностную схему в произвольных точках ?) да ?) нет Вопрос id:1639660 Явная разностная схема является условно устойчивой ?) да ?) нет Вопрос id:1639661 Верно ли высказывание? А) В общем случае граница решений задачи является криволинейной, а не квадратом или прямоугольником В) В общем случае граница решений задачи является квадратом или прямоугольником ?) А – да, В – да ?) А – да, В – нет ?) А – нет, В – нет ?) А – нет, В – да Вопрос id:1639662 Верно ли утверждение? А) Приближенные методы решения наиболее разработаны для дифференциальных уравнений в частных производных второго порядка с двумя независимыми переменными В) Линейные или вполне линейные дифференциальные уравнения в частных производных содержат произведение производных искомой функции ?) А – да, В – нет ?) А – нет, В – да ?) А – да, В – да ?) А – нет, В – нет Вопрос id:1639663 Верны ли утверждения? А) Для получения повышенной точности при численном интегрировании пользуются формулой Гаусса В) В формуле Гаусса не фиксируются квадратурные коэффициенты ?) А – да, В – нет ?) А – да, В – да ?) А – нет, В – нет ?) А – нет, В – да Вопрос id:1639664 Верны ли утверждения? А) Задача решения обыкновенных дифференциальных уравнений сложнее задачи вычисления однократных интегралов В) Доля задач, интегрируемых в явном виде, существенно меньше ?) А – да, В – да ?) А – да, В – нет ?) А – нет, В – да ?) А – нет, В – нет Вопрос id:1639665 Верны ли утверждения? А) При решении дифференциального уравнения методом Рунге-Кутта необходимо производить много вычислений для нахождения В) На практике применяется метод Адамса, который не требует многократного подсчета правой части уравнения ?) А – да, В – нет ?) А – да, В – да ?) А – нет, В – нет ?) А – нет, В – да Вопрос id:1639666 Верны ли утверждения? Практические вычисления разностей требуют наличие контролирующих операций на всех этапах. К контролирующей операции при составлении таблицы конечных разностей можно отнести свойство: А) Сумма чисел в каждом столбце разностей равна разности крайних чисел предыдущего столбца В) Произведение чисел в каждом столбце разностей равна произведению крайних чисел предыдущего столбца ?) А – нет, В – да ?) А – да, В – да ?) А – нет, В – нет ?) А – да, В – нет Вопрос id:1639667 Верны ли утверждения? А) Абсолютная погрешность округления не превосходит половины единицы разряда, определяемого последней оставленной значащей цифрой В) При округлении приближенного числа получается новое приближенное число, абсолютная погрешность которого складывается из абсолютной погрешности первоначального числа и погрешности округления ?) А – нет, В – да ?) А – нет, В – нет ?) А – да, В – нет ?) А – да, В – да Вопрос id:1639668 Верны ли утверждения? А) В методе касательных при выборе начального приближения корня за исходную точку надо выбирать тот конец отрезка В) В методе касательных при выборе начального приближения корня за исходную точку надо выбирать тот конец отрезка ?) А – нет, В – да ?) А – да, В – да ?) А – да, В – нет ?) А – нет, В – нет Вопрос id:1639669 Верны ли утверждения? А) В методе хорд неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной В) В методе хорд неподвижным концом отрезка является тот, для которого знак функции противоположен знаку второй производной ?) А – нет, В – да ?) А – нет, В – нет ?) А – да, В – нет ?) А – да, В – да Вопрос id:1639670 Верны ли утверждения? А) Если математик не участвует в обсуждении физической постановки задачи, то представление о величине неустранимой погрешности ему не нужно знать В) Имея представление о величине неустранимой погрешности, математик-исследователь может разумно сформулировать требования к точности результата численного решения задачи ?) А – нет, В – да ?) А – да, В – да ?) А – нет, В – нет ?) А – да, В – нет Вопрос id:1639671 Верны ли утверждения? А) Комбинированный метод удобен при оценке погрешности вычислений В) При комбинированном методе истинный корень заключен между приближенными корнями, получающимися по методу хорд и методу касательных ?) А – да, В – да ?) А – да, В – нет ?) А – нет, В – да ?) А – нет, В – нет Вопрос id:1639672 Верны ли утверждения? А) Конечно-разностные аппроксимации для частных производных являются наиболее распространенным подходом к численному интегрированию дифференциальных уравнений в частных производных В) В общем случае размерность области, в которой необходимо найти решение дифференциального уравнения в частных производных, равна числу независимых переменных ?) А – да, В – нет ?) А – нет, В – да ?) А – да, В – да ?) А – нет, В – нет Вопрос id:1639673 Верны ли утверждения? А) Математик всегда может производить необходимые упрощения исходной задачи В) Анализ влияния различных факторов на погрешность решения может позволить получить простейшее описание процесса с допустимой погрешностью ?) А – нет, В – нет ?) А – да, В – нет ?) А – да, В – да ?) А – нет, В – да Вопрос id:1639674 Верны ли утверждения? А) Неустранимая погрешность неконтролируема в процессе численного решения задачи В) Неустранимая погрешность может уменьшиться только за счет более точного определения параметров задачи ?) А – нет, В – нет ?) А – да, В – да ?) А – да, В – нет ?) А – нет, В – да Вопрос id:1639675 Верны ли утверждения? А) Обобщением понятия производной является понятие разделенной разности В) При фиксированных ?) А – да, В – да ?) А – нет, В – нет ?) А – да, В – нет ?) А – нет, В – да Вопрос id:1639676 Верны ли утверждения? А) Ограничения на порядки чисел в компьютере иногда приводят к прекращению вычислений либо к недопустимому искажению результата вычислительной погрешностью В) Явление «потери значащих цифр» имеют место при вычитании близких значений. Это явление часто приводит к существенному искажению результата при решении систем линейных алгебраических уравнений ?) А – да, В – нет ?) А – нет, В – да ?) А – да, В – да ?) А – нет, В – нет Вопрос id:1639677 Верны ли утверждения? А) Относительную погрешность часто выражают в процентах В) Выражение «функция сильно растет» чаще всего означает, что она возрастает в очень большое число раз ?) А – да, В – нет ?) А – да, В – да ?) А – нет, В – нет ?) А – нет, В – да Вопрос id:1639678 Верны ли утверждения? А) Повышение точности интегрирования иногда достигается за счет разбиения отрезка на равные части В) Если подынтегральная функция или её производные невысокого порядка имеют участки резкого изменения, например, обращаются в бесконечность, то такие функции плохо приближаются многочленами сразу на всем отрезке интегрирования ?) А – да, В – нет ?) А – нет, В – нет ?) А – нет, В – да ?) А – да, В – да Вопрос id:1639679 Верны ли утверждения? А) Погрешность математической модели может уменьшиться только за счет более точного описания физической задачи В) Вычислительная погрешность может возникнуть из-за конечности количества разрядов чисел, участвующих в вычислениях ?) А – да, В – нет ?) А – нет, В – нет ?) А – да, В – да ?) А – нет, В – да Вопрос id:1639680 Верны ли утверждения? А) Постоянный множитель можно выносить за знак разделенной разности В) Постоянный множитель нельзя выносить за знак разделенной разности ?) А – да, В – нет ?) А – нет, В – нет ?) А – нет, В – да ?) А – да, В – да Вопрос id:1639681 Верны ли утверждения? А) При более детальном подходе к изучению задачи в целом оказывается, что столь высокая точность и не нужна В) Даже если математическая модель настолько груба, все равно есть смысл требовать высокую точность решения задачи ?) А – да, В – да ?) А – да, В – нет ?) А – нет, В – да ?) А – нет, В – нет Вопрос id:1639682 Верны ли утверждения? А) При конечно-разностной аппроксимации частные производные заменяются соответствующими разностными соотношениями по соответствующим независимым переменным В) В случае двух независимых переменных область решений является двумерным ?) А – да, В – да ?) А – нет, В – нет ?) А – да, В – нет ?) А – нет, В – да Вопрос id:1639683 Верны ли утверждения? А) При практическом анализе погрешности численного интегрирования часто пользуются различными полуэмпирическими приемами. В) В настоящее время важнейшей проблемой является создание систем решения задач с максимально простым обращением, предполагающих малую квалификацию пользователя в отношении численных методов и программирования ?) А – нет, В – да ?) А – да, В – да ?) А – да, В – нет ?) А – нет, В – нет Вопрос id:1639684 Верны ли утверждения? А) При решении задач часто приходится вычислять производную В) Если функция задана таблично, то методы дифференциального исчисления к исследованию таких функций применить нельзя ?) А – да, В – да ?) А – нет, В – да ?) А – да, В – нет ?) А – нет, В – нет Вопрос id:1639685 Верны ли утверждения? А) Приближения покоординатного спуска минимизации функции и метода Зейделя решения системы совпадают В) Приближения покоординатного спуска минимизации функции и метода Зейделя решения системы не совпадают ?) А – нет, В – нет ?) А – да, В – нет ?) А – да, В – да ?) А – нет, В – да Вопрос id:1639686 Верны ли утверждения? А) Разделенная разность есть симметрическая функция своих аргументов В) Метод, требующий меньшего количества арифметических операций, не всегда является лучшим ?) А – да, В – нет ?) А – нет, В – нет ?) А – нет, В – да ?) А – да, В – да Вопрос id:1639687 Верны ли утверждения? А) Разделенные разности порядка В) Разделенные разности порядка больше ?) А – да, В – да ?) А – да, В – нет ?) А – нет, В – нет ?) А – нет, В – да Вопрос id:1639688 Верны ли утверждения? А) Решение уравнения Лапласа может быть получено аналитически В) При аналитическом решении уравнения Лапласа используются только численные методы ?) А – да, В – нет ?) А – да, В – да ?) А – нет, В – да ?) А – нет, В – нет Вопрос id:1639689 Верны ли утверждения? А) Степень многочлена, для которого точна квадратура, определяется числом свободных параметров квадратуры В) Не существует квадратур с N узлами, точных для всех тригонометрических многочленов степени N ?) А – да, В – нет ?) А – нет, В – нет ?) А – да, В – да ?) А – нет, В – да Вопрос id:1639690 Верны ли утверждения? А) Узлы интерполяции, лежащие ближе к интерполируемому значению В) Узлы интерполяции, лежащие ближе к интерполируемому значению ?) А – да, В – нет ?) А – да, В – да ?) А – нет, В – да ?) А – нет, В – нет Вопрос id:1639691 Верны ли утверждения? А) Часто математик сам занимается исследованием постановки задачи, анализом и упрощением рассматриваемых уравнений В) Поскольку все явления в природе взаимосвязаны, в принципе невозможно математически точно описать никакой реальный процесс, происходящий в природе ?) А – да, В – нет ?) А – нет, В – да ?) А – да, В – да ?) А – нет, В – нет Вопрос id:1639692 Вычисления по методу Рунге-Кутта удобно располагать по схеме в таблицу.
Установите порядок действий при вычислении по методу Рунге-Кутта ?) Полученное значение 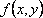 столбца 4 умножают на шаг интегрирования столбца 4 умножают на шаг интегрирования 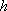 и вычисляют и вычисляют  и записывают в столбец 5 этой же строки. Найденные значения и записывают в столбец 5 этой же строки. Найденные значения 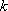 умножают на соответствующий коэффициент (на 1 , если это умножают на соответствующий коэффициент (на 1 , если это  или или 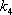 , или на 2, если это , или на 2, если это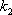 или или  ) и результат записывают в столбец 6 текущей строки. ) и результат записывают в столбец 6 текущей строки.?) В столбцы таблицы 2 и 3 текущей строки записывают нужные значения  и и 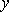 . Если строка первая, то записывают начальные данные . Если строка первая, то записывают начальные данные 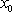 и и 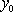 . .?) Значения  и и  текущей строки подставляют в правую часть дифференциального уравнения текущей строки подставляют в правую часть дифференциального уравнения  и определяют и определяют 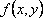 и записывают в столбец 4 этой же строки и записывают в столбец 4 этой же строки?) Результат 6 столбца суммируют, делят на 6 и определяют 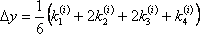 и и 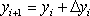 .Затем все вычисления повторяют, начиная с 1-го шага, до тех пор, пока не будет пройден весь отрезок .Затем все вычисления повторяют, начиная с 1-го шага, до тех пор, пока не будет пройден весь отрезок 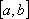 Вопрос id:1639693 Найти многочлен наименьшей степени, который в заданных точках имеет заданные значения
?)  ?) 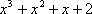 ?) 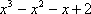 ?) 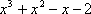 Вопрос id:1639694 При решении математических задач получаются приближенные результаты в силу различных причин. Установите соответствие между понятиями и причинами
Вопрос id:1639695 Функция
?)  ?) 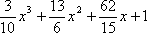 ?)  ?) 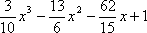 Вопрос id:1639696 Абсолютная погрешность алгебраической суммы нескольких приближенных чисел ___ суммы абсолютных погрешностей этих чисел ?) превышает ?) строго меньше ?) равно ?) не превышает Вопрос id:1639697 Анализ усложненных моделей явления потребовал создания специальных ?) численных методов решения задачи ?) методик разработки математических моделей явления ?) новых алгоритмов исследования явлений ?) новых методик исследования явлений природы Вопрос id:1639698 В вычислительной практике часто приходится иметь дело с функциями, заданными таблично для некоторого конечного множества значений аргумент, например 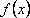 , а в процессе применения надо знать значение функции , а в процессе применения надо знать значение функции 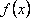 для промежуточных значений аргумента. В этом случае строят функцию для промежуточных значений аргумента. В этом случае строят функцию 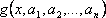 достаточно простую, которая в заданных в таблице точках принимаете же значения, что и функция достаточно простую, которая в заданных в таблице точках принимаете же значения, что и функция  , а в остальных точках приближенно равна ей. Задача построения такой функции , а в остальных точках приближенно равна ей. Задача построения такой функции  называется ___ называется ___?) абсолютным приближением ?) максимальным приближением ?) экстраполированием ?) интерполированием Вопрос id:1639699 В десятичной системе счисления значение каждой цифры в числе зависит от её положения среди других цифр этого числа, поэтому эта система счисления является ___ Вопрос id:1639700 В методе Рунге-Кутта вместо непосредственных вычислений 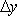 определяются четыре числа определяются четыре числа?) 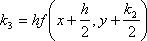 ; ; 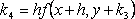 ?) 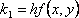 ; ; 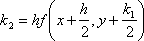 ?)  ; ; 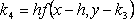 ?) 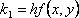 ; ; 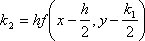 |

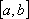 , в котором знак функции совпадает со знаком второй производной
, в котором знак функции совпадает со знаком второй производной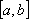 , в котором знак функции противоположен знаку второй производной
, в котором знак функции противоположен знаку второй производной разделенная разность является линейным функционалом от функции
разделенная разность является линейным функционалом от функции 
 (т.е. не меняется при любой их перестановке)
(т.е. не меняется при любой их перестановке) от многочлена
от многочлена  -й степени постоянны
-й степени постоянны  от многочлена
от многочлена  -й степени равны нулю
-й степени равны нулю  , окажут большее влияние на интерполяционный многочлен, узлы, лежащие дальше, - меньшее
, окажут большее влияние на интерполяционный многочлен, узлы, лежащие дальше, - меньшее  , окажут меньшее влияние на интерполяционный многочлен, узлы, лежащие дальше, - большее
, окажут меньшее влияние на интерполяционный многочлен, узлы, лежащие дальше, - большее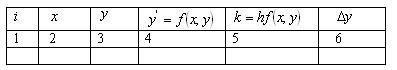

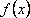 задана таблично
задана таблично  Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа  имеет вид
имеет вид