Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
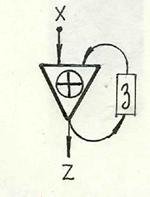
Список вопросов базы знанийДискретная математика (курс 2)Вопрос id:737142 Для автомата с матрицей переходов  графом переходов является ?)  ?)  ?)  Вопрос id:737143 Выход функционального элемента логической сети может быть присоединен A) к входу другого функционального элемента В) к выходу сети ?) A – нет, B – нет ?) A – да, B – нет ?) A – да, B – да ?) A – нет, B – да Вопрос id:737144 Выход функционального элемента логической сети может быть присоединен A) к выходу другого функционального элемента В) к выходу сети ?) A – нет, B – нет ?) A – нет, B – да ?) A – да, B – нет ?) A – да, B – да Вопрос id:737145 Пусть r(X) означает: «Х – действительное число», q(X) : «X – рациональное число». Тогда формула: А) ∀Х (r(X) → q(X)) выражает истинное высказывание В) ∃Х (r(X) → q(X)) выражает истинное высказывание ?) A – да, B – да ?) A – да, B – нет ?) A – нет, B – да ?) A – нет, B – нет Вопрос id:737146 Пусть r(X) означает: «Х – действительное число», q(X) : «X – рациональное число». Тогда формула: А) ∀Х (q(X) → r(X)) выражает истинное высказывание В) ∀Х (r(X) → q(X)) выражает истинное высказывание ?) A – нет, B – нет ?) A – нет, B – да ?) A – да, B – да ?) A – да, B – нет Вопрос id:737147 Пусть r(X) означает: «Х – действительное число», q(X) : «X – рациональное число». Тогда формула: А) ∀Х (q(X) → r(X)) выражает истинное высказывание В) ∃Х (q(X) → r(X)) выражает истинное высказывание ?) A – нет, B – нет ?) A – нет, B – да ?) A – да, B – да ?) A – да, B – нет Вопрос id:737148 Пусть r(X) означает: «Х – действительное число», q(X) : «X – рациональное число». Тогда формула: А) ∃Х (q(X) → r(X)) выражает истинное высказывание В) ∃Х (r(X) → q(X)) выражает истинное высказывание ?) A – нет, B – да ?) A – нет, B – нет ?) A – да, B – нет ?) A – да, B – да Вопрос id:737149
Выходная последовательность Z(t): На вход логической сети подается последовательность Х(t) = 0, 0, 0, 1, ?) 1, 1, 1, 1, 1, 1, 1, 1, . . . ?) 0, 0, 0, 1, 0, 0, 0, 1, . . . ?) 0, 0, 0, 1, . . . 0, 0, 0, 1, 1, 1, 1, 1, . . . ?) 1, 0, 0, 0, 1, 0, 0, 0, . . . Вопрос id:737150 В графе переходов автомата с входным алфавитом {a, b, с, d, e}, выходным алфавитом {a, b, c} и 10 состояниями A) число вершин равно 10 В) число дуг (без склеивания) равно 50 ?) A – нет, B – да ?) A – да, B – нет ?) A – нет, B – нет ?) A – да, B – да Вопрос id:737151 В графе переходов автомата с входным алфавитом {a, b, с, d}, выходным алфавитом {a, b} и 6 состояниями A) число вершин равно 4 В) число дуг (без склеивания) равно 24 ?) A – нет, B – нет ?) A – нет, B – да ?) A – да, B – да ?) A – да, B – нет Вопрос id:737152 В графе переходов автомата с входным алфавитом {a, b}, выходным алфавитом {a, b, c, d} и 5 состояниями A) число вершин равно 5 В) число дуг (без склеивания) равно 20 ?) A – нет, B – да ?) A – да, B – да ?) A – да, B – нет ?) A – нет, B – нет Вопрос id:737153 Для истинности сложного высказывания «Если присяжные вынесут обвинительный вердикт, то защита подаст апелляцию» истинность простого высказывания «Защита подаст апелляцию» является A) необходимым условием В) достаточным условием ?) A – да, B – нет ?) A – да, B – да ?) A – нет, B – да ?) A – нет, B – нет Вопрос id:737154 Для истинности сложного высказывания «Если присяжные вынесут обвинительный вердикт, то защита подаст апелляцию» истинность простого высказывания «Присяжные вынесут обвинительный вердикт» является A) необходимым условием В) достаточным условием ?) A – да, B – да ?) A – да, B – нет ?) A – нет, B – нет ?) A – нет, B – да Вопрос id:737155 На вход логической сети подается последовательность Х(t) = 0, 0, 1, 0, 0, 1, 0, 0, 1, . . . Выходная последовательность Z(t) ?) 1, 0, 0, 0, 1, 0, 0, 0, 1, . . . ?) 0, 0, 1, 0, 0, 1, 0, 0, 1, . . . ?) 0, 0, 0, 1, 0, 0, 0, 1, 0, . . . ?) 0, 0, 1, 1, 1, 1, 1, 1, 1, . . . Вопрос id:737156 На вход логической сети подается последовательность Х(t) = 1, 0, 1, 0, 1, 0, 1, 0, . . .
Выходная последовательность Z(t): ?) 1, 1, 0, 0, 1, 1, 0, 0, . . . ?) 1, 1, 1, 0, 1, 1, 1, 0, . . . ?) 0, 1, 0, 1, 0, 1, 0, 1, . . . ?) 1, 0, 0, 0, 1, 0, 0, 0, . . . Вопрос id:737157 На вход логической сети подается последовательность Х(t) = 1, 1, 1, 1,
?) 1, 1, 1, 1, 1, 1, 1, 1, 1, . . . ?) 1, 0, 0, 0, 1, 0, 0, 0, 1, . . . ?) 0, 0, 1, 0, 0, 1, 0, 0, 1, . . . ?) 0, 0, 0, 0, 0, 0, 0, 0, 0, . . . Вопрос id:737158  - двуместный предикат (X, Y – целые числа). Истинность высказывания∀ X, Y: P(X, Y) равна?) 1 ?) 0, если X ≠ Y ?) 1, если X ≠ Y ?) зависит от знаков чисел X, Y Вопрос id:737159 X = {x} – множество птиц, Y = {y} – множество летающих животных. Соотношение «все птицы летают, но некоторые летающие животные – не птицы» записывается формулой ?) (∀y: y ⊂ X) & (∃x: x ⊂ Y) ?) (∀x: x ⊂ Y) ↔ (∃y: y ∉ X) ?) (∃x: x ⊂ Y) & (∀y: y ∉ X) ?) (∀y: y ⊂ X) & (∃x: x ∉ Y) Вопрос id:737160 X = {x} – множество птиц, Y = {y} – множество летающих животных. Соотношение «если все птицы летают, то все летающие животные – птицы» записывается формулой ?) (∀x: x ⊂ Y) ↔ (∀y: y ⊂ X) ?) (∀x: х ⊂ Y) → (∀y: y ⊂ X) ?) ∃x: x ⊂ Y) → (∀y: y ⊂ X) ?) (∃x: x ⊂ Y) ↔ (∀y: y ⊂ X) Вопрос id:737161 X = {x} – множество птиц, Y = {y} – множество летающих животных. Соотношение «если все птицы летают, то некоторые летающие животные – не птицы» записывается формулой ?) (∃x: x ⊂ Y) & (∀y: y ⊂ X) ?) (∃x: x ⊂ Y) → (∀y: y ⊂ X) ?) (∀x: х ⊂ Y) → (∃y: y ∉ X) ?) (∀x: x ⊂ Y) ↔ (∀y: y ∉ X) Вопрос id:737162 X = {x} – множество птиц, Y = {y} – множество летающих животных. Соотношение «некоторые птицы не летают, но все летающие животные – птицы» записывается формулой ?) (∃ y: y ⊂ X) ↔ (∃x: x ∉ Y) ?) (∃x: x ∉ Y) ↔ (∃y: y ∉ X) ?) (∀y: y ⊂ X) ↔ (∃x: x ⊂ Y) ?) (∃x: х ∉ Y) ↔ (∀y: y ⊂ X) Вопрос id:737163 X – множество студентов группы, Y – множество дисциплин, по которым сдают экзамен. Высказывание «Eсть студент, не сдавший ни одного экзамена» выражается предикатной формулой ?) ∃Y ∀X: (P(X, Y) = 0) ?) ∀Y ∃X: (P(X, Y) = 0) ?) ∀X ∃Y: (P(X, Y) = 0) ?) ∃X ∀Y: (P(X, Y) = 0) Вопрос id:737164 X – множество студентов группы, Y – множество дисциплин, по которым сдают экзамен. Предикат P(X, Y) : «студент Х сдал экзамен по дисциплине Y». Предикатная формула ∀X: P(X, Y) означает ?) некоторые студенты сдали экзамен по предмету Y ?) Х сдал экзамен хотя бы по одному предмету ?) Х сдал экзамен по всем предметам ?) все студенты сдали экзамен по предмету Y Вопрос id:737165 В графе переходов (без склеивания дуг) автомата с входным алфавитом {a, b, c, d, e, f}, выходным алфавитом {a, d, е, g, h} и 4 состояниями число дуг, исходящих из каждой вершины, равно ?) 4 ?) 5 ?) 6 ?) 24 Вопрос id:737166 В графе переходов (без склеивания дуг) автомата с входным алфавитом {a, b, c, d, e}, выходным алфавитом {a, d, е, g} и 6 состояниями число дуг, исходящих из каждой вершины, равно ?) 6 ?) 4 ?) 30 ?) 5 Вопрос id:737167 В графе переходов (без склеивания дуг) автомата с входным алфавитом {a, b, c}, выходным алфавитом {a, d, е, g, h} и 7 состояниями число дуг, исходящих из каждой вершины, равно ?) 3 ?) 21 ?) 7 ?) 5 Вопрос id:737168 Диаграмма Венна  изображает соотношения ?) все X суть Y; ни одно X не есть Z; ни одно Z не есть Y ?) все Y суть X; ни одно X не есть Z; ни одно Z не есть Y ?) все X суть Y; некоторые Z суть Y; ни одно X не есть Z ?) некоторые X суть Y; ни одно Y не есть Z; некоторые Z суть X Вопрос id:737169 Диаграмма Венна  изображает соотношения?) все X суть Y; некоторые Z суть Y; все X суть Z ?) все Y суть X; некоторые Z суть X; некоторые Y суть Z ?) все X суть Y; некоторые X суть Z; некоторые Z суть Y ?) некоторые X суть Y; все Y суть Z; некоторые Z суть X Вопрос id:737170 Для автомата с матрицей переходов  графом переходов является ?)  ?)  ?)  ?)  Вопрос id:737171 Для истинности сложного высказывания X & Y истинность простого высказывания Х является условием ?) не является ни необходимым, ни достаточным ?) необходимым, но недостаточным ?) необходимым и достаточным ?) достаточным, но не необходимым Вопрос id:737172 Для истинности сложного высказывания X → Y истинность простого высказывания Y является условием ?) не является ни необходимым, ни достаточным ?) необходимым, но недостаточным ?) необходимым и достаточным ?) достаточным, но не необходимым Вопрос id:737173 Для множеств  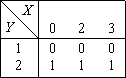и  предикат  : " – четное число" может быть представлен таблицей?)  ?)  ?)  ?)  Вопрос id:737174 Для того чтобы произведение целых чисел a • b было нечетным, условие «a или b – нечетное» является ?) не является ни необходимым, ни достаточным ?) необходимым, но не достаточным ?) необходимым и достаточным ?) достаточным, но не необходимым Вопрос id:737175 Для того чтобы произведение целых чисел a • b было четным, условие «a или b – четное» является ?) не является ни необходимым, ни достаточным ?) необходимым и достаточным ?) необходимым, но не достаточным ?) достаточным, но не необходимым Вопрос id:737176 Для того чтобы сумма целых чисел a + b была четной, условие «a и b – оба четные» является ?) необходимым, но не достаточным ?) достаточным, но не необходимым ?) необходимым и достаточным ?) не является ни необходимым, ни достаточным Вопрос id:737177 Для того чтобы сумма целых чисел a + b была нечетной, условие «a и b – оба нечетные» является ?) необходимым и достаточным ?) достаточным, но не необходимым ?) не является ни необходимым, ни достаточным ?) необходимым, но не достаточным Вопрос id:737178 Канонические уравнения автомата выражают внутреннее состояние автомата в следующий момент через ?) предыдущее значение на входе и предыдущее внутреннее состояние ?) текущее значение на входе и предыдущее внутреннее состояние ?) текущее значение на входе и текущее внутреннее состояние ?) предыдущее значение на входе и текущее внутреннее состояние Вопрос id:737179 Канонические уравнения автомата выражают текущее выходное значение через ?) текущее значение на входе и текущее внутреннее состояние ?) предыдущее значение на входе и текущее внутреннее состояние ?) предыдущее значение на входе и предыдущее внутреннее состояние ?) текущее значение на входе и предыдущее внутреннее состояние Вопрос id:737180 Матрица переходов автомата с входным алфавитом {a, b, c, d}, выходным алфавитом {d, е} и 7 состояниями имеет размерность ?) 7 х 4 ?) 2 х 4 ?) 4 х 7 ?) 7 х 2 Вопрос id:737181 Матрица переходов автомата с входным алфавитом {a, b, c}, выходным алфавитом {a, b, c, d, е, f} и 4 состояниями имеет размерность ?) 3 х 6 ?) 4 х 3 ?) 4 х 6 ?) 6 х 4 Вопрос id:737182 Матрица переходов автомата с входным алфавитом {a, b}, выходным алфавитом {a, b, d} и 9 состояниями имеет размерность ?) 9 х 9 ?) 2 х 9 ?) 9 х 2 ?) 9 х 3 Вопрос id:737183 Минимальное число задержек при реализации автомата с 10 состояниями логической сетью равно ?) 5 ?) 3 ?) 4 ?) 10 Вопрос id:737184 Минимальное число задержек при реализации автомата с 14 состояниями логической сетью равно ?) 2 ?) 7 ?) 4 ?) 5 Вопрос id:737185 Минимальное число задержек при реализации автомата с 5 состояниями логической сетью равно ?) 2 ?) 3 ?) 5 ?) 4 Вопрос id:737186 На вход автомата с входным алфавитом A = {a1, a2, a3}, выходным алфавитом B = {b1, b2}, множеством внутренних состояний Q = {q1, q2, q3, q4, q5} подается входная периодическая последовательность с периодом Т = 7. Выходная последовательность имеет период ?) 21 ?) 7 ?) 14 ?) 35 Вопрос id:737187 На вход автомата с входным алфавитом A = {a1, a2, a3}, выходным алфавитом B = {b1, b2}, множеством внутренних состояний Q = {q1, q2, q3, q4} подается входная периодическая последовательность с периодом Т = 5. Выходная последовательность имеет период ?) 5 ?) 15 ?) 10 ?) 20 Вопрос id:737188 На вход автомата с входным алфавитом A = {a1, a2, a3}, выходным алфавитом B = {b1, b2}, множеством внутренних состояний Q = {q1, q2, q3, q4, q5, q6, q7} подается входная периодическая последовательность с периодом Т = 5. Выходная последовательность имеет период ?) 15 ?) 5 ?) 35 ?) 10 Вопрос id:737189 На вход автомата с входным алфавитом A = {a1, a2, a3}, выходным алфавитом B = {b1, b2}, множеством внутренних состояний Q = {q1, q2, q3, q4, q5} подается входная периодическая последовательность с периодом Т = 7 и предпериодом 2. Выходная последовательность имеет полный период ?) 16 ?) 23 ?) 9 ?) 37 Вопрос id:737190 На вход автомата с входным алфавитом A = {a1, a2, a3}, выходным алфавитом B = {b1, b2}, множеством внутренних состояний Q = {q1, q2, q3, q4} подается входная периодическая последовательность с периодом Т = 6 и предпериодом 5. Выходная последовательность имеет полный период ?) 23 ?) 11 ?) 17 ?) 29 Вопрос id:737191 На вход логической сети подается последовательность Х(t) = 0, 0, 0, 0, 0, 0, . . .  Выходная последовательность Z(t) ?) 1, 0, 1, 0, 1, 0, . . . ?) 1, 0, 0, 0, 1, 0, . . . ?) 1, 1, 1, 0, 1, 1, . . . ?) 0, 1, 0, 1, 0, 1, . . . |
Copyright testserver.pro 2013-2024