Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийВведение в теорию случайных процессов
Вопрос id:1606406 Имеется система масcового обслуживания с неограниченной очередью, n - число каналов, l - интенсивность потока заявок, m - интенсивность потока обслуживания, r - загрузка системы, pn - вероятность того, что заняты все каналы и нет очереди; тогда среднее число заявок в очереди ?) 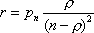 ?) 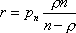 ?)  ?) 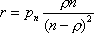 Вопрос id:1606407 Имеется система масcового обслуживания с неограниченной очередью, n - число каналов, l - интенсивность потока заявок, m - интенсивность потока обслуживания, r - загрузка системы, pn - вероятность того, что заняты все каналы и нет очереди; тогда среднее время ожидания в очереди ?) 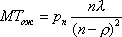 ?) 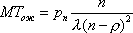 ?) 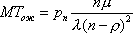 ?) 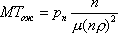 Вопрос id:1606408 Имеется система масcового обслуживания с неограниченной очередью, n - число каналов, l - интенсивность потока заявок, m - интенсивность потока обслуживания, r - загрузка системы, pn - вероятность того, что заняты все каналы и нет очереди; тогда среднее число занятых каналов ?) z = r ?) z = lpn ?)  ?) z = mpn 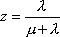Вопрос id:1606409 Имеется система масcового обслуживания с неограниченной очередью, n - число каналов, l - интенсивность потока заявок, m - интенсивность потока обслуживания, r - загрузка системы, pn - вероятность того, что заняты все каналы и нет очереди; тогда среднее время пребывания в системе ?) 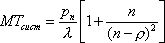 ?)  ?) 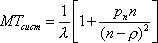 ?) 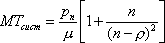 Вопрос id:1606410 Имеется система масового обслуживания с неограниченной очередью, n - число каналов, l - интенсивность потока заявок, m - интенсивность потока обслуживания, r - загрузка системы, pn - вероятность того, что заняты все каналы и нет очереди; тогда среднее число заявок в системе ?) 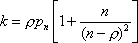 ?) 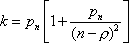 ?) 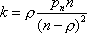 ?)  Вопрос id:1606411 Имеется система с отказами и n каналами, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r, средним числом заявок в очереди r и вероятностью того, что система свободна p0, тогда показатели эффективности работы системы таковы: вероятность того, что система свободна ?) 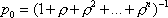 ?) 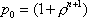 ?) 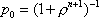 ?)  Вопрос id:1606412 Имеется система с отказами и n каналами, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r, средним числом заявок в очереди r и вероятностью того, что система свободна p0, тогда показатели эффективности работы системы таковы: относительная пропускная способность ?) 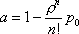 ?) 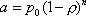 ?) 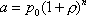 ?) 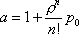 Вопрос id:1606413 Имеется система с отказами и n каналами, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r, средним числом заявок в очереди r и вероятностью того, что система свободна p0, тогда показатели эффективности работы системы таковы: абсолютная пропускная способность ?) 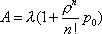 ?) 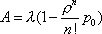 ?) 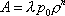 ?) 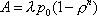 Вопрос id:1606444 Имеется система с отказами и n каналами, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r, средним числом заявок в очереди r и вероятностью того, что система свободна p0, тогда показатели эффективности работы системы таковы: среднее число занятых каналов ?) 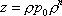 ?) 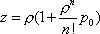 ?)  ?)  Вопрос id:1606445 Имеется система с отказами и n каналами, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r, средним числом заявок в очереди r и вероятностью того, что система свободна p0, тогда показатели эффективности работы системы таковы: вероятность отказа ?) 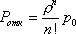 ?) 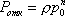 ?) 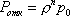 ?)  Вопрос id:1606446 Интенсивность потока заявок в системе массового обслуживания - это ?) среднее число заявок, приходящих в систему за единицу времени ?) доля обслуженных заявок среди поступивших ?) число заявок, приходящих в систему за время ее работы ?) среднее число обслуженных заявок в единицу времени Вопрос id:1606447 Ковариационная функция B(t) стационарного случайного процесса как функция аргумента t является ?) периодической ?) нечетной ?) четной ?) возрастающей Вопрос id:1606448 Ковариационная функция B(t) стационарного случайного процесса при t = 0 равна ?) дисперсии этого процесса ?) постоянной величине ?) нулю ?) периодической функции Вопрос id:1606449 Ковариационная функция случайного процесса X(t) определяется формулой ?) B(t, s) = cov[X(t), X(t)2] ?) B(t, s) = cov[X(t - s), X(t + s)] ?) B(t, s) = cov[X(t), X(t + s)] ?) B(t, s) = cov[X(t), X(s)] Вопрос id:1606450 Конечномерным распределением случайного процесса в моменты t1, …, tn называется распределение многомерной случайной величины, составленной в моменты t1, …, tn из ?) математических ожиданий ?) траекторий ?) сечений ?) дисперсий Вопрос id:1606451 Линейный прогноз 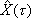 называют оптимальным (наилучшим) для случайного процесса X(t), если на нем минимальна величина?) 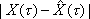 ?) 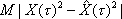 ?) 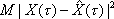 ?) 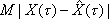 Вопрос id:1606452 Линейный прогноз является наилучшим из возможных для процессов ?) стационарных ?) с независимыми приращениями ?) гауссовских ?) марковских Вопрос id:1606453 Марковский случайный процесс обладает следующим свойством: ?) это процесс с дискретным временем ?) это процесс с независимыми значениями ?) при известном настоящем его будущее не зависит от прошлого ?) его конечномерные распределения нормальны Вопрос id:1606454 Математическое ожидание случайного процесса Z(t) = Xt + Yt2, где MX = 3, MY = -2, равно ?) 3 - 2t ?) 3t + 2t2 ?) 3t - 2t2 ?) 6t Вопрос id:1606455 Математическое ожидание стационарного случайного процесса есть ?) постоянная величина ?) периодическая функция ?) нечетная функция ?) положительная величина Вопрос id:1606456 Множество возможных значений случайного процесса называется ?) фазовым пространством ?) пространством элементарных событий ?) конечномерным распределением ?) законом распределения Вопрос id:1606457 Модуль ковариационной функции B(t) стационарного случайного процесса достигает при t = 0 ?) наибольшего значения ?) нуля ?) любого промежуточного значения ?) наименьшего значения Вопрос id:1606458 Наибольший средний выигрыш в управляемом марковском процессе достигается на стратегии ?) наилучшей ?) принятой ?) оптимальной ?) допустимой Вопрос id:1606459 Оценка 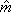 для математического ожидания m стационарного случайного процесса, если известна реализация процесса x(t), при t Î [0; T], и имеет вид?) 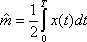 ?) 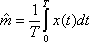 ?)  ?) 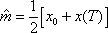 Вопрос id:1606460 Оценка 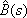 для корреляционной функции B(s) стационарного случайного процесса, если известна реализация процесса x(t) при t Î [0; T], имеет вид?) 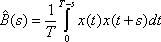 ?) 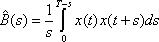 ?)  ?) 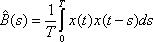 Вопрос id:1606461 Поток является простейшим, если он обладает свойствами: 1) стационарность; 2) непрерывность; 3) ординарность; 4) дискретность; 5) стохастичность; 6) отсутствие последействия ?) 2, 4, 6 ?) 3, 4, 5 ?) 1, 2, 3 ?) 1, 3, 6 Вопрос id:1606462 При решении задач оптимального линейного прогнозирования считают известной, по крайней мере, ?) ковариационную функцию ?) конечномерные распределения ?) траектории процессов ?) математическое ожидание и дисперсию Вопрос id:1606463 Прогноз неизвестных значений стационарного случайного процесса есть функция от ?) корреляционной функции случайного процесса ?) известных значений случайного процесса ?) последней по времени реализации ?) траекторий случайного процесса Вопрос id:1606464 Производительность канала системы массового обслуживания M и среднее время обслуживания MTобсл. связаны соотношением ?) MTобсл. = e-m ?) MTобсл. = ln/u ?) MTобсл. = m ?) MTобсл. =  Вопрос id:1606465 Промежуток времени T между соседними событиями простейшего потока имеет функцию распределения ?) логнормальную ?) нормальную ?) Коши ?) показательную Вопрос id:1606466 Простейший поток является ?) биномиальным ?) пуассоновским ?) потоком Бернулли ?) гауссовским Вопрос id:1606467 Реализация случайного процесса - это ?) неслучайная функция ?) неизвестная функция ?) константа ?) случайная функция Вопрос id:1606468 Самая элементарная классификация случайных процессов - по ?) «времени» и «состояниям» ?) «состояниям» и «математическим ожиданиям» ?) «математическим ожиданиям» и «дисперсиям» ?) «времени» и «математическим ожиданиям» Вопрос id:1606469 Связь между абсолютной A и относительной пропускной способностью a системы, где l - интенсивность потока заявок, выражается соотношением ?) 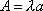 ?) 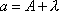 ?)  ?) 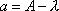 Вопрос id:1606470 Семейство реализаций случайного процесса может быть получено в результате ?) построения графиков распределений ?) составления конечномерных распределений ?) вычисления числовых характеристик случайного процесса ?) нескольких стохастических экспериментов Вопрос id:1606471 Сечение случайного процесса X(t) = j(t, w) получается при ?) фиксированном w = w0 ?) фиксированных t = t0 и w = w0 ?) вычислении математического ожидания ?) фиксированном t = t0 Вопрос id:1606472 Системы массового обслуживания предназначены для многократного проведения некоторой однотипной элементарной операции, которая называется операцией ?) ожидания ?) обслуживания ?) действия ?) развития Вопрос id:1606473 Случайная последовательность - это случайный процесс ?) с независимыми значениями ?) со временем на конечном отрезке ?) с дискретным временем ?) с непрерывным временем Вопрос id:1606474 Случайный процесс X(t) = 2Vt, где V - случайная величина, имеющая стандартно нормальное распределение. Его дисперсия s2(t) равна ?) 4 ?) 4t2 ?) 2t2 ?) 2t Вопрос id:1606475 Случайный процесс X(t) = 3Vt, где V - случайная величина, имеющая стандартно нормальное распределение. Его ковариация B(t,s) равна ?) 3ts ?) 9ts ?) 3(t + s) ?) 3(t - s)2 Вопрос id:1606476 Случайный процесс X(t) = Vt + 5, где V(t) - случайная величина, имеющая стандартно нормальное распределение, f(x, t) - плотность распределения сечения этого процесса имеет вид ?) 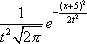 ?) 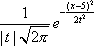 ?) 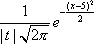 ?) 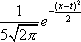 Вопрос id:1606477 Случайный процесс X(t) = Vt - 1, где V(t) - случайная величина, имеющая стандартно нормальное распределение. Его математическое ожидание m(t) равно ?) + 1 ?) t - 1 ?) - 1 ?) t + 1 Вопрос id:1606478 Случайный процесс называется гауссовским, если все его конечномерные распределения являются ?) нормальными ?) биномиальными ?) распределениями Пуассона ?) распределениями Эрланга Вопрос id:1606479 Случайным процессом X(t) называется процесс, значение которого при любом фиксированном t = t0 является ?) непрерывной функцией ?) числом ?) случайной величиной ?) постоянной функцией Вопрос id:1606480 Среднее время между соседними событиями простейшего потока с параметром l равно ?) 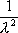 ?) 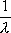 ?) l2 ?) l Вопрос id:1606481 Среднее число заявок, которое может обслужить система массового обслуживания, есть ?) интенсивность потока обслуживания ?) абсолютная пропускная способность ?) интенсивность потока заявок ?) относительная пропускная способность Вопрос id:1606482 Среднее число событий простейшего потока с параметром l, наступивших за единицу времени, равно ?)  ?) l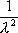2 ?)  ?) l Вопрос id:1606483 Средний суммарный выигрыш в управляемом марковском процессе является функцией от ?) траектории процесса ?) переходной функции ?) выбранной стратегии ?) первого принятого решения Вопрос id:1606484 Цена «предприятия по эксплуатации» системы, соответствующей управляемому марковскому процессу, - это значение суммарного выигрыша на стратегии ?) наихудшей ?) оптимальной ?) наилучшей ?) допустимой Вопрос id:1606485 Классификацию систем массового обслуживания проводят в зависимости от: 1) количества каналов обслуживания; 2) наличия или отсутствия очереди; 3) характера ожидания заявок в очереди; 4) интенсивности потока заявок; 5) интенсивности потока обслуживания; 6) пропускной способности системы ?) 1, 2, 3 ?) 1, 2, 5, 6 ?) 1, 3, 4, 6 ?) 1, 2, 3, 4, 5, 6
|
Copyright testserver.pro 2013-2024