Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийВведение в теорию случайных процессов
Вопрос id:1606326 В многоканальной системе массового обслуживания n каналов, длина очереди ограничена величиной m; загрузка системы - r; вероятность того, что система свободна, - p0; l и m соответственно интенсивности потока заявок и потока обслуживания. Размеченный граф состояний системы имеет вид ?) 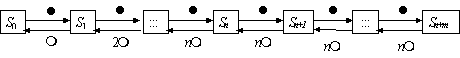 ?) 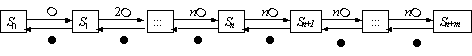 ?) 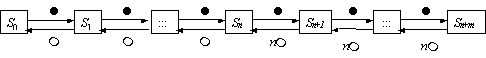 ?) 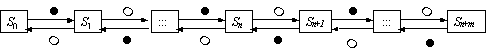 Вопрос id:1606327 В многоканальной системе массового обслуживания n каналов, длина очереди ограничена величиной m; загрузка системы - r; вероятность того, что система свободна, - p0; l и m соответственно интенсивности потока заявок и потока обслуживания. Вероятность отказа системы ?) 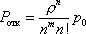 ?) 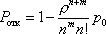 ?) 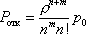 ?) 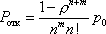 Вопрос id:1606328 В многоканальной системе массового обслуживания n каналов, длина очереди ограничена величиной m; загрузка системы - r; вероятность того, что система свободна, - p0; l и m соответственно интенсивности потока заявок и потока обслуживания. Относительная пропускная способность системы a равна ?) 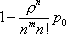 ?) 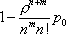 ?) 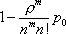 ?) 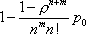 Вопрос id:1606329 В многоканальной системе массового обслуживания n каналов, длина очереди ограничена величиной m; загрузка системы - r; вероятность того, что система свободна, - p0; l и m соответственно интенсивности потока заявок и потока обслуживания. Абсолютная пропускная способность системы A равна ?) 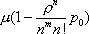 ?) 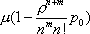 ?) 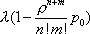 ?) 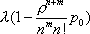 Вопрос id:1606330 В многоканальной системе массового обслуживания n каналов, длина очереди ограничена величиной m; загрузка системы - r; вероятность того, что система свободна, - p0; l и m соответственно интенсивности потока заявок и потока обслуживания. Среднее число заявок в очереди r равно ?) 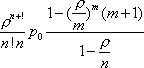 ?) 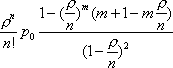 ?) 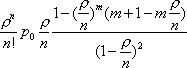 ?) 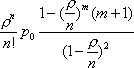 Вопрос id:1606331 В многоканальной системе массового обслуживания n каналов, длина очереди ограничена величиной m; загрузка системы - r; вероятность того, что система свободна, - p0; l и m соответственно интенсивности потока заявок и потока обслуживания. Среднее число заявок в системе ?) 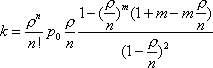 ?) 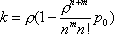 ?) 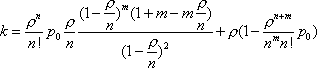 ?) 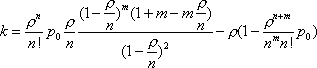 Вопрос id:1606332 В одноканальной системе с ограниченной очередью длиной m, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна, и r - среднее число заявок в очереди показатели эффективности работы системы массового обслуживания таковы: относительная пропускная способность ?) a = 1 - 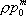 ?) a = rm+1p0 ?) a = 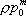 ?) a = 1 - rm+1p0 Вопрос id:1606333 В одноканальной системе с ограниченной очередью длиной m, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна, и r - среднее число заявок в очереди показатели эффективности работы системы массового обслуживания таковы: абсолютная пропускная способность ?) A = 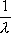 (1 - rm + 1p0) (1 - rm + 1p0)?) A = l(1 - rm + 1p0) ?) A = 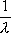 rm + 1p0 rm + 1p0?) A = lrm + 1p0 Вопрос id:1606334 В одноканальной системе с ограниченной очередью длиной m, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна и r - среднее число заявок в очереди, показатели эффективности работы системы массового обслуживания таковы: среднее число заявок r, находящихся в очереди, равно ?) 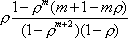 ?) 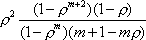 ?) 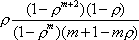 ?) 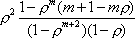 Вопрос id:1606335 В одноканальной системе с ограниченной очередью длиной m, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна, r - среднее число заявок в очереди показатели эффективности работы системы массового обслуживания таковы: среднее время ожидания в очереди ?) 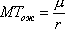 ?) 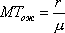 ?) 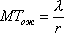 ?) 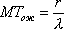 Вопрос id:1606336 В одноканальной системе с ограниченной очередью длиной m, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна и r - среднее число заявок в очереди, показатели эффективности работы системы массового обслуживания таковы: среднее время пребывания заявки в системе ?) 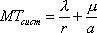 ?) 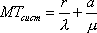 ?) 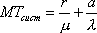 ?) 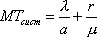 Вопрос id:1606337 В одноканальной системе с ограниченной очередью длиной m, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна, r - среднее число заявок в очереди показатели эффективности работы системы массового обслуживания следующие: вероятность того, что система свободна, такова ?) p0 = (1 + rm)-1 ?) p0 = 1 + r + r2 + … + rm +1 ?) p0 = (1 + r + r2 + … + rm +1)-1 ?) p0 = (1 + r2 + r4 + … + r2m)-1 Вопрос id:1606338 В одноканальной системе с ограниченной очередью длиной m, интенсивностью потока заявок l, нитенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна, r - среднее число заявок в очереди показатели эффективности работы системы массового обслуживания таковы: среднее число заявок ?) k = r - 1 + p0 ?) k = r - 1 - p0 ?) k = r + 1 - p0 ?) k = r + 1 + p0 Вопрос id:1606339 В одноканальной системе с отказами, интенсивностью m потока обслуживания и l - потока заявок показатели эффективности работы системы массового обслуживания таковы: относительная пропускная способность a равна ?) 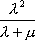 ?) 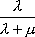 ?) 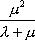 ?) 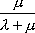 Вопрос id:1606340 В одноканальной системе с отказами, интенсивностью m потока обслуживания и l - потока заявок показатели эффективности работы системы массового обслуживания таковы. Абсолютная пропускная способность A равна ?) 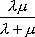 ?) l(l + m) ?) m(l + m) ?) 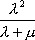 Вопрос id:1606341 В одноканальной системе с отказами, интенсивностью m потока обслуживания и l - потока заявок показатели эффективности работы системы массового обслуживания таковы. Вероятность отказа Pотк ?) 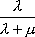 ?) 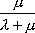 ?) 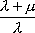 ?) 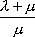 Вопрос id:1606342 В одноканальной системе с отказами, интенсивностью m потока обслуживания и l - потока заявок предельные вероятности состояний таковы ?) 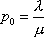 ; ; 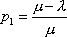 ?) 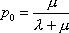 ; ; 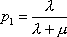 ?) 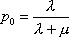 ; ; 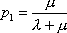 ?) 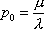 ; ; 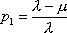 Вопрос id:1606343 В одноканальной системе с отказами, которая свободна в начальный момент времени, вероятности состояний таковы ?) 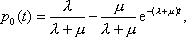 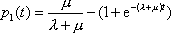 ?) 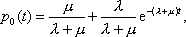 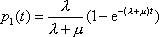 ?) 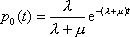 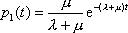 ?) p0(t) = le-(l+ m)t p1(t) = 1 - le-(l+ m)t Вопрос id:1606344 В управляемом марковском процессе решение есть функция от ?) переходной функции случайного процесса ?) реализации случайного процесса ?) предельных вероятностей состояний процесса ?) состояний случайного процесса Вопрос id:1606345 В управляемом марковском процессе стратегию образуют (образует) ?) решения, принимаемые в начале процесса управления ?) совокупность траекторий управляемого случайного процесса ?) последовательность значений переходных функций ?) совокупность решений, принимаемых на каждом шаге управления Вопрос id:1606346 Вероятность потерь по времени системы с отказами, где n - число пришедших требований, w - число потерянных требований среди пришедших, есть ?) 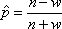 ?) 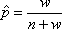 ?) 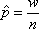 ?) 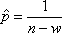 Вопрос id:1606350 Вероятность потерь по времени системы с отказами, где t3 - отрезок времени, когда система была полностью занята, за время наблюдения t, есть ?) 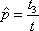 ?) 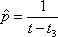 ?) 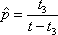 ?) 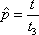 Вопрос id:1606378 Вероятность того, что за единицу времени наступило k событий простейшего потока интенсивности l, равна ?) 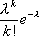 ?) 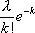 ?) 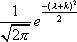 ?) 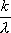 Вопрос id:1606379 Входящим потоком называется множество моментов ?) начала обслуживания поступивших требований ?) времени между поступлением и началом обслуживания требований ?) поступления требований в систему ?) окончания обслуживания поступивших требований Вопрос id:1606380 Дисперсия времени между соседними событиями простейшего потока с параметром l равна ?) 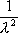 ?) l ?) 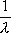 ?) l2 Вопрос id:1606381 Дисперсия числа событий простейшего потока с параметром l, наступивших за единицу времени, равна ?) 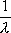 ?) l2 ?) 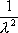 ?) l Вопрос id:1606382 Дифференциальные уравнения Колмогорова для вероятностей состояний системы 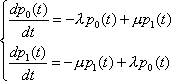 соответствуют графу состояний соответствуют графу состояний?)  ?) 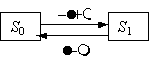 ?) 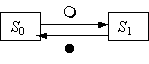 ?)  Вопрос id:1606383 Доля обслуженных заявок среди поступивших в систему - это ?) интенсивность потока обслуживания ?) абсолютная пропускная способность ?) относительная пропускная способность ?) интенсивность потока заявок Вопрос id:1606384 Если X(t) - случайный процесс с дискретным временем, то его дисперсия есть неотрицательная ?) случайная величина ?) детерминированная величина ?) последовательность функций ?) последовательность чисел Вопрос id:1606385 Если X(t) - случайный процесс с дискретным временем, то математическое ожидание есть ?) числовой ряд ?) число ?) вектор ?) последовательность чисел Вопрос id:1606386 Если X(t) - случайный процесс с непрерывным временем, то его математическое ожидание есть ?) векторная функция ?) числовая функция ?) случайная величина ?) случайная функция Вопрос id:1606387 Если X(t) - случайный процесс с непрерывным временем, то его дисперсия есть ?) постоянная функция ?) непрерывная функция ?) случайная величина ?) неотрицательная числовая функция Вопрос id:1606388 Если в системе массового обслуживания интенсивность потока заявок l, интенсивность потока обслуживания m, то загрузка системы ?) 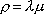 ?) 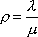 ?) 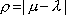 ?) 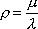 Вопрос id:1606389 Если имеется одноканальная система с ограниченной очередью длиной m, интенсивностью потока заявок l, интенсивностью потока обслуживания m, то ей соответствует размеченный граф состояний ?) 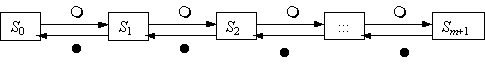 ?) 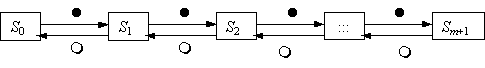 ?) 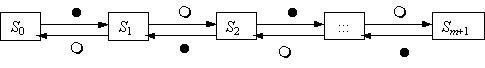 ?) 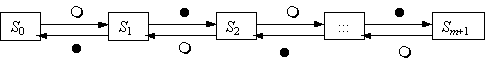 Вопрос id:1606390 Если имеется система с n каналами, с отказами, интенсивностью потока заявок l и интенсивностью потока обслуживания m, то ей соответствует граф состояний ?) 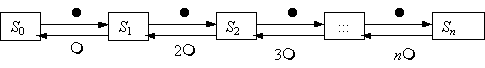 ?) 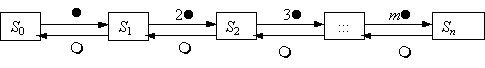 ?) 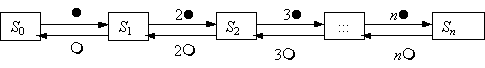 ?) 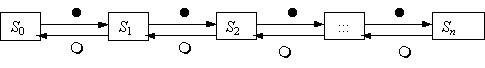 Вопрос id:1606391 Если поток - простейший с интенсивностью l, то среднее число событий, наступающих за время t, вычисляется по формуле ?) MX(t) = 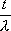 ?) MX(t) = l × t ?) MX(t) = e-lt ?) MX(t) =  Вопрос id:1606392 Задачи управления марковскими процессами решаются с помощью уравнения ?) Лапласа ?) Гаусса ?) Фурье ?) Беллмана Вопрос id:1606393 Имеется N наблюдений одноканальной системы с неограниченной очередью, ui - число обслуженных требований, ui - число поступивших требований, 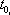 - общее время, когда система свободна за время наблюдения t, i - номер наблюдения; тогда оценка интенсивности входящего потока - общее время, когда система свободна за время наблюдения t, i - номер наблюдения; тогда оценка интенсивности входящего потока?) 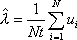 ?) 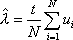 ?) 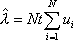 ?) 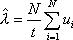 Вопрос id:1606394 Имеется N наблюдений одноканальной системы с неограниченной очередью, ui - число обслуженных требований, ui - число поступивших требований, 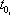 - общее время, когда система свободна за время наблюдения t, i - номер наблюдения; тогда оценка интенсивности потока обслуживания - общее время, когда система свободна за время наблюдения t, i - номер наблюдения; тогда оценка интенсивности потока обслуживания?) 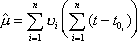 ?) 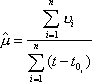 ?) 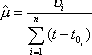 ?) 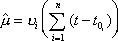 Вопрос id:1606395 Имеется наблюдение в течение времени t над n-канальной системой с очередью длины m, u - число поступивших заявок, принятых на обслуживание, tn+m - общее время полной занятости системы; тогда оценка интенсивности входящего потока ?) 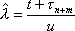 ?) 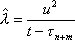 ?) 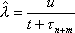 ?) 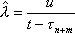 Вопрос id:1606396 Имеется наблюдение в течение времени t над n-канальной системой с очередью длины m; u - число обслуженных заявок, cn - суммарное время, затраченное на обслуживание всех u заявок; тогда оценка интенсивности потока обслуживания ?) 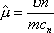 ?) 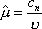 ?) 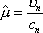 ?) 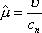 Вопрос id:1606397 Имеется одно наблюдение одноканальной системы с неограниченной очередью, t0 - общее время, когда система свободна, u - число обслуженных требований, а u - число требований, поступивших в систему за время наблюдения t; тогда оценка интенсивности входящего потока ?) 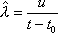 ?) 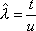 ?) 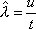 ?) 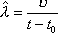 Вопрос id:1606398 Имеется одно наблюдение одноканальной системы с неограниченной очередью: t0 - общее время, когда система свободна, (0, t) - отрезок времени наблюдения, u - число обслуженных требований, а u - число поступивших требований, n - начальное число требований; тогда оценка интенсивности входящего потока ?) 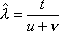 ?) 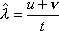 ?) 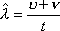 ?) 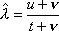 Вопрос id:1606399 Имеется одно наблюдение одноканальной системы с неограниченной очередью: t0 - общее время, когда система свободна, (0, t) - отрезок времени наблюдения, u - число обслуженных требований, а u - число поступивших требований, n - начальное число требований; тогда оценка интенсивности потока обслуживания ?) 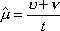 ?) 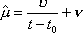 ?) 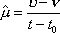 ?) 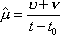 Вопрос id:1606400 Имеется одно наблюдение одноканальной системы с неограниченной очередью: t0 - общее время, когда система свободна, u - число обслуженных требований, а u - число требований, поступивших в систему за время наблюдения t; тогда оценка интенсивности потока обслуживания ?) 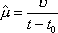 ?) 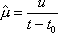 ?) 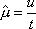 ?) 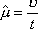 Вопрос id:1606401 Имеется система масcового обслуживания с неограниченной очередью, n - число каналов, l - интенсивность потока заявок, m - интенсивность потока обслуживания, r - загрузка системы, pn - вероятность того, что заняты все каналы и нет очереди; тогда условие существования стационарного режима имеет вид ?) l < n ?) r < l ?) r < n ?) l < m Вопрос id:1606402 Имеется система масcового обслуживания с неограниченной очередью, n - число каналов, l - интенсивность потока заявок, m - интенсивность потока обслуживания, r - загрузка системы, pn - вероятность того, что заняты все каналы и нет очереди; тогда вероятность отказа ?) Pотк = Pn ?) Pотк = 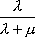 ?) Pотк =  ?) Pотк = 0 Вопрос id:1606403 Имеется система масcового обслуживания с неограниченной очередью, n - число каналов, l - интенсивность потока заявок, m - интенсивность потока обслуживания, r - загрузка системы, pn - вероятность того, что заняты все каналы и нет очереди; тогда относительная пропускная способность ?) a = l ?) a = 1 ?) a = m ?) a = 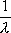 Вопрос id:1606404 Имеется система масcового обслуживания с неограниченной очередью, n - число каналов, l - интенсивность потока заявок, m - интенсивность потока обслуживания, r - загрузка системы, pn - вероятность того, что заняты все каналы и нет очереди; тогда абсолютная пропускная способность ?) A = r ?) A = l ?) A = l + m ?) A = m Вопрос id:1606405 Имеется система масcового обслуживания с неограниченной очередью, n - число каналов, l - интенсивность потока заявок, m - интенсивность потока обслуживания, r - загрузка системы, pn - вероятность того, что заняты все каналы и нет очереди; тогда вероятность того, что заняты все каналы и нет очереди ?) 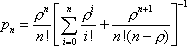 ?) 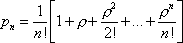 ?) 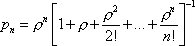 ?) 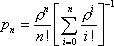
|
Copyright testserver.pro 2013-2024