Вход | Регистрация

Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.

Вход в систему

Список вопросов базы знаний

Введение в теорию игр и вероятности (профильный курс)

Страница:
1
2

Вопрос id:1606296

Лампочки изготавливаются независимо друг от друга. В среднем одна лампочка из тысячи оказывается бракованной. Найдите вероятность того, что из двух взятых наугад лампочек окажутся исправными обе

?) 0.9

?) 0.9999

?) 0.998001

?) 0.98

Вопрос id:1606297

Монету бросали 100 раз. 70 раз выпал орел, для проверки гипотезы о симметричности монеты строим доверительный интервал и проверяем, попали ли мы в него. Найдите формулу, по которой строится доверительный интервал, и определите проверку в нашем конкретном случае

?) I _0,95 (p) =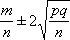

, монета не симметричная

?) I _0,95 (p) =

, монета симметричная

?) I _0,95(p) =

, монета симметричная

?) I _0,95 (p) =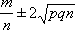

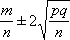, монета не симметричная

Вопрос id:1606298

На некоторой фабрике машина А производит 40% продукции, а машина B - 60%. В среднем 9 из 1000 единиц продукции, произведенных машиной А, и 1 из 250, произведенных машиной B, оказываются бракованными. Определите вероятность, что случайно выбранная единица продукции окажется бракованной

?) 0.007

?) 0.006

?) 0.5

?) 0.008

Вопрос id:1606299

На некотором заводе было замечено, что при определенных условиях в среднем 1.6% изготовленных изделий оказываются неудовлетворяющими стандарту и идут в брак. Определите вероятность того, что наугад взятое изделие этого завода окажется качественным и количество, примерно, непригодных изделий (назовем это число M) в партии из 1000 изделий

?) p = 0.16; M = 16

?) p = 0.984; M = 16

?) р = 1.6; M = 16

?) p = 0.016; M = 160

Вопрос id:1606300

На отрезке длиной 20 см помещен меньший отрезок L длиной 10 см. Найти вероятность того, что точка, наудачу поставленная на большой отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения

?) 0.1

?) 1/4

?) 0.5

?) 0.2

Вопрос id:1606301

Найдите вероятность достоверного события

?) 1

?) 0.1

?) Может быть любым числом

?) 0

Вопрос id:1606302

Найдите вероятность невозможного события

?) 1

?) 0

?) 0.5

?) Может быть любым числом

Вопрос id:1606303

При изготовлении детали заготовка должна пройти четыре операции. Полагая появление брака на отдельных операциях событиями независимыми, найти (с точностью до 4-х знаков после запятой) вероятность изготовления нестандартной детали, если вероятность брака на первой стадии операции равна 0.02, на второй - 0.01, на третьей - 0.02, на четвертой - 0.03

?) 0.0777

?) 0.0800

?) 0.9200

?) 0.9222

Вопрос id:1606304

Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении прибора - 0.03, второго - 0.06. Найти вероятность того, что при включении прибора откажет только второй элемент

?) 0.0582

?) 0.0671

?) 0.0938

?) 0.06

Вопрос id:1606305

Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении прибора - 0.05, второго - 0.08. Найти вероятность того, что при включении прибора оба элемента будут работать

?) 0.928

?) 0.874

?) 0.826

?) 0.871

Вопрос id:1606306

Проверяется гипотеза о том, что вероятность выиграть в рулетку 1/37. Доверительный интервал с уровнем доверия 95% строится по формуле

, где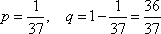

, n - число испытаний, m - количество выигрышей. Найдите число ставок (т.е. каким взять n), которое надо сделать, чтобы отношение числа выигрышей (m к числу n), отличалось от 1/37 не более, чем на 0,01

?) n =100

?) n =500

?) n =900

?) n =10

Вопрос id:1606307

Производится n независимых испытаний, в которых вероятность наступления события A равна p. n велико. Вероятность того, что событие A наступит m раз, вычисляется по формуле или используются асимптотические приближения

?) по формуле Байеса

?) используются асимптотические приближения

?) вычисляется по формуле p(1-p)

?) вычисляется по формуле Бернулли

Вопрос id:1606308

Производится n независимых испытаний, в которых вероятность наступления события A равна p. Вероятность того, что событие A наступит m раз

?) вычисляется по формуле Байеса

?) равна p(1-p)

?) вычисляется по формуле Бернулли

?) вычисляется по формуле Муавра-Лапласа

Вопрос id:1606309

Рабочий обслуживает три станка. Вероятность того, что в течение часа станок потребует внимания рабочего, равна для первого станка 0.1, для второго - 0.2 и для третьего - 0.15. Найти вероятность того, что в течение некоторого часа хотя бы один из станков потребует внимания рабочего

?) 0.388

?) 0.635

?) 0.365

?) 0.612

Вопрос id:1606310

Рулетка размечается с помощью меток - 00, 0, 1, ...36. Метки при игре не имеют преимуществ друг перед другом. Игрок делает 114 попыток. Найдите вероятность ни разу не выиграть

?) 0.03

?) 0.05

?) 0.08

?) 0.07

Вопрос id:1606311

С первого станка на сборку поступает 40% деталей, остальные 60% со второго. Вероятность изготовления бракованной детали для первого и второго станка соответственно равна 0.01 и 0.04. Найдите вероятность того, что наудачу поступившая на сборку деталь окажется бракованной

?) 0.028

?) 0.024

?) 0.032

?) 0.022

Вопрос id:1606312

Случайная величина X принимает значения 7, -2, 1, -5, 3 с равными вероятностями. Найдите MX

?) 0.8

?) 0.7

?) 0.9

?) 0

Вопрос id:1606313

События A и B называются несовместными, если

?) р(AB)=р(+р(B)

?) р(AB)=1

?) р(AB)=0

?) р(AB)=р(р(B)

Вопрос id:1606314

События называются независимыми, если

?) р(AB)=р(/р(B)

?) р(AB)=р(B)/р(

?) р(AB)=р(р(B)

?) р(AB)=р(+р(B)

Вопрос id:1606315

Станок-автомат производит изделия трех сортов. Первого сорта - 80%, второго - 15%. Определите вероятность того, что наудачу взятое изделие будет или второго, или третьего сорта

?) 0.8

?) 0.2

?) 0.95

?) 0.15

Вопрос id:1606316

Страхуется 1600 автомобилей; вероятность того, что автомобиль может попасть в аварию, равна 0.2. Определите асимптотическое приближение, чтобы сосчитать вероятность того, что число аварий не превысит 350

?) надо сосчитать по формуле Бернулли, асимптотические формулы дадут большую ошибку

?) интегральной формулой Муавра-Лапласа

?) распределением Пуассона

?) локальной формулой Муавра-Лапласа

Вопрос id:1606317

Стрелок попадает в цель в среднем в 8 случаях из 10. Найдите вероятность, что, сделав три выстрела, он два раза попадет

?) 0.384

?) 0.314

?) 0.392

?) 0.324

Вопрос id:1606318

Студенту предлагают 6 вопросов и на каждый вопрос 4 ответа, из которых один верный, и просят дать верные ответы. Студент не подготовился и выбирает ответы наугад. Найдите вероятность того, что он правильно ответит ровно на половину вопросов (С точностью до 3-х знаков после запятой)

?) 0.256

?) 0.164

?) 0.112

?) 0.132

Вопрос id:1606319

Теннисист идет на игру. Если ему дорогу перебежит черная кошка, то вероятность победы 0,2; если не перебежит, то - 0,7. Вероятность, что кошка перебежит дорогу - 0,1; что не перебежит - 0,9. Вероятность победы

?) 0,1·0,8+0,9·0,3

?) 0,9·0,2+0,1·0,7

?) 0,1·0,2+0,9·0,7

?) 0,1·0,2·0,9·0,7

Вопрос id:1606320

Условной вероятностью события B при условии, что событие A с ненулевой вероятностью произошло, называется

?) р(B/=р(AB)/р(B)

?) р(B/=р(AB)/р(

?) р(B/=р(AB)р(

?) р(B/=р(AB)

Вопрос id:1606321

Человеку, достигшему 20-летнего возраста, вероятность умереть в течение 20 лет равна 0.02. Найдите вероятность того, что из 200 застраховавшихся на 20 лет человек в возрасте 20 лет ни один не умрет

?) 0.0183

?) 0.0145

?) 0.0235

?) 0.256

Вопрос id:1606322

Человеку, достигшему 20-летнего возраста, вероятность умереть на 21-м году жизни равна 0,01. Найдите вероятность того, что из 200 застраховавшихся человек в возрасте 20-ти лет один умрет через год

?) 0.246

?) 0.271

?) 0.256

?) 0.297

Вопрос id:1606323

Человеку, достигшему 60-летнего возраста, вероятность умереть на 61-м году жизни равна 0.09. Найдите вероятность того, что из трех человек в возрасте 60 лет ни один не будет жив через год

?) 0.000713

?) 0.000729

?) 0.999886

?) 0.999271

Вопрос id:1606324

Человеку, достигшему 60-летнего возраста, вероятность умереть на 61-м году жизни равна 0.09. Найдите вероятность того, что из трех человек в возрасте 60 лет хотя бы один умрет через год

?) 0.9100

?) 0.2464

?) 0.7536

?) 0.8281

Вопрос id:1606325

Число грузовых машин, проезжающих мимо бензоколонки, относится к числу легковых машин, как 3:2. Известно, что в среднем одна из 30 грузовых и одна из 25 легковых машин останавливается для заправки. Найти вероятность того, что проезжающая машина будет заправляться

?) 0.04

?) 0.036

?) 0.33

?) 0.5

Страница:
1
2