Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийВведение в теорию игр и вероятности (профильный курс)
Вопрос id:1606246 DX = 1.5. Используя свойства дисперсии, найдите D(2X+5) ?) 6 ?) 3 ?) 8 ?) 11 Вопрос id:1606247 MX = 1.5. Используя свойства математического ожидания, найдите M(2X+5) ?) 5 ?) 8 ?) 6.5 ?) 3 Вопрос id:1606248 MX = 5, MY = 2. Используя свойства математического ожидания, найдите M(2X - 3Y) ?) 3 ?) 5 ?) 2 ?) 4 Вопрос id:1606249 X и Y - независимы. DX = 5, DY = 2. Используя свойства дисперсии, найдите D(2X+3Y) ?) 26 ?) 16 ?) 38 ?) 30 Вопрос id:1606250 Бросается 5 монет. Найдите вероятность того, что три раза выпадет герб ?) 5/16 ?) 11/16 ?) 17/32 ?) 15/32 Вопрос id:1606251 Бросается 6 монет. Вероятность того, что герб выпадет более четырех раз равна ?) 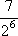 ?)  ?) 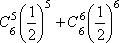 ?) 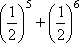 Вопрос id:1606252 Бросаются 2 кубика. Вероятность, что сумма выпавших очков равна 3, составит ?) 1/6 ?) 1/18 ?) 1/3 ?) 3/36 Вопрос id:1606253 Бросаются 2 монеты. Вероятность того, что выпадут и герб, и решка, равна ?) 1/4 ?) 0.3 ?) 1/3 ?) 0.5 Вопрос id:1606254 Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти вероятность того, что пуля попадет в один из белых секторов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры. ?) 0.75 ?) 0.5 ?) 0.4 ?) 0.25 Вопрос id:1606255 В группе 25 студентов, из которых отлично учится 5 человек, хорошо - 12, удовлетворительно - 6 и слабо - 2. Преподаватель вызывает студента. Определите вероятность того, что вызванный студент или отличник или хорошист ?) 0.5 ?) 8/25 ?) 17/25 ?) 0.85 Вопрос id:1606256 В круг радиусом 10 помещен меньший круг радиусом 5. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения ?) 0.5 ?) 0.75 ?) 0.25 ?) 0.05 Вопрос id:1606257 В круг радиусом 20 см помещен меньший круг радиусом 10 см так, что их центры совпадают. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения ?) 0.4 ?) 0.25 ?) 0.5 ?) 0.75 Вопрос id:1606258 В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.95, из обычной винтовки - 0.7. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена ?) 0.9 ?) 0.85 ?) 0.83 ?) 0.87 Вопрос id:1606259 В среднем каждое сотое изделие, производимое предприятием, дефектное. Если взять два изделия, определите вероятность, что оба окажутся исправными ?) 0.01 ?) 0.213 ?) 0.9801 ?) 0.001 Вопрос id:1606260 В ящике в 5 раз больше красных шаров, чем черных. Найти вероятность p того, что вынутый наугад шар окажется красным ?) 5/6 ?) 0.5 ?) 0.6 ?) 1/6 Вопрос id:1606261 Вероятность выиграть в кости равна 1/6. Игрок делает 120 ставок. Определите асимптотическое приближение, чтобы сосчитать вероятность того, что число выигрышей не будет меньше 15 ?) интегральной формулой Муавра-Лапласа ?) надо сосчитать по формуле Бернули ?) локальной формулой Муавра-Лапласа ?) распределением Пуассона Вопрос id:1606262 Вероятность выиграть в рулетку равна 1/38. Игрок делает 190 ставок. Вероятность того, что он выиграет не менее 5 раз можно найти с помощью ?) надо сосчитать по формуле Бернулли, асимптотические формулы дадут большую ошибку ?) плотности нормального распределения ?) распределения Пуассона ?) функции Лапласа Ф(х) Вопрос id:1606263 Вероятность выиграть, играя в рулетку, 1/37. Сделав ставку 100 раз, мы ни разу не выиграли. Заподозрив, что игра ведется не честно, мы решили проверить свою гипотезу, построив 95%-ый доверительный интервал для вероятности выигрыша. Найдите формулу, по котрой строится интервал и определите проверку в нашем случае ?) 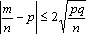 , игра нечестная , игра нечестная?) 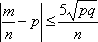 , игра честная , игра честная?) 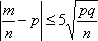 , игра честная , игра честная?) 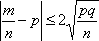 , игра честная , игра честнаяВопрос id:1606264 Вероятность любого события всегда удовлетворяет следующему условию ?) может принять любое значение ?) может принимать значения, меньшие 0 ?) она не меньше 0 и не больше 1 ?) всегда строго больше 0 Вопрос id:1606265 Вероятность появлений события А в испытании равна p. Найдите дисперсию числа появлений события А в одном испытании ?) 1/p ?) p(1-p) ?) 1-p ?) p Вопрос id:1606266 Вероятность появления события А в испытании равна 0.1. Найдите среднеквадратическое отклонение числа появлений события А в одном испытании ?) 0.9 ?) 0.09 ?) 0.3 ?) 0.03 Вопрос id:1606267 Вероятность суммы любых случайных событий A и B вычисляется по формуле ?) р(A+B)=р(AB) ?) р(A+B)=р(+р(B)-2р(AB) ?) р(A+B)=р(+р(B) ?) р(A+B)=р(+р(B)-р(AB) Вопрос id:1606268 Вероятность того, что дом может сгореть в течение года, равна 0.01. Застраховано 500 домов. Определите асимптотическое приближение, чтобы сосчитать вероятность того, что сгорит не более 5 домов ?) локальной формулой Муавра-Лапласа ?) интегральной формулой Муавра-Лапласа ?) распределением Пуассона ?) надо сосчитать по формуле Бернулли, асимптотические формулы дадут большую ошибку Вопрос id:1606269 Вероятность того, что размеры детали, выпускаемой станком-автоматом, окажутся в пределах заданных допусков, равна 0.96. Определите процент брака q и количество негодных деталей в среднем (назовем это число M), которое будет содержаться в каждой партии объемом 500 штук ?) q = 0.4%; M = 496 ?) q = 96%; M = 480 ?) q = 4%; M = 20 ?) q = 0.96%; M = 40 Вопрос id:1606270 Возможные значения случайной величины X таковы: x1 = 2, x2 = 5, x3 = 8. Известны вероятности: р(X = 2) = 0.4; р(X = 5) = 0.15. Найдите р(X = 8) ?) 0.4 ?) 0.55 ?) 0.45 ?) 0.5 Вопрос id:1606271 Вратарь парирует в среднем 30 % всех одиннадцатиметровых штрафных ударов. Найдите вероятность того, что он возьмет ровно два из четырех мячей ?) 0.2811 ?) 0.3248 ?) 0.3145 ?) 0.2646 Вопрос id:1606272 Выпущено 100 лотерейных билетов, причем установлены призы, из которых 8 по 1 руб., 2 - по 5 руб. и 1 - 10 руб. Найдите вероятности p0 (билет не выиграл), p1 (билет выиграл 1 руб.), p5 (билет выиграл 5 руб.) и p10 (билет выиграл 10 руб.) событий. ?) p0=0.9; p1=0.08; p5=0.02; p10=0.01 ?) p0=0.88; p1=0.08; p5=0.02; p10=0.01 ?) p0=0.89 p1=0.08; p5=0.01; p10=0.02 ?) p0=0.89; p1=0.08; p5=0.02; p10=0.01 Вопрос id:1606273 Два стрелка стреляют по мишени. Вероятность попадания в цель у одного стрелка 0.7, у другого - 0.8. Найти вероятность того, что цель будет поражена ?) 0.8 ?) 0.96 ?) 0.85 ?) 0.94 Вопрос id:1606274 Два стрелка стреляют по разу в общую цель. Вероятность попадания в цель у одного стрелка 0.6, у другого - 0.7. Найти вероятность того, что цель будет поражена двумя пулями ?) 0.96 ?) 0.88 ?) 0.56 ?) 0.42 Вопрос id:1606275 Два стрелка стреляют по разу в общую цель. Вероятность попадания в цель у одного стрелка 0.8, у другого - 0.9. Найти вероятность того, что цель не будет поражена ни одной пулей ?) 0.96 ?) 0.02 ?) 0.72 ?) 0.98 Вопрос id:1606276 Для вероятности р по выборке объема n с помощью величены 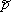 и таблиц нормального распределения строится доверительный интервал. Если увеличить объем выборки в 100 раз, длина доверительного интервала примерно и таблиц нормального распределения строится доверительный интервал. Если увеличить объем выборки в 100 раз, длина доверительного интервала примерно?) уменьшится в 10 раз ?) уменьшится в 100 раз ?) увеличится в 100 раз ?) увеличится в 10 раз Вопрос id:1606277 Для контроля качества продукции завода из каждой партии готовых изделий выбирают для проверки 1000 деталей. Проверку не выдерживают в среднем 80 изделий. Определите вероятность того, что наугад взятое изделие этого завода окажется качественным и количество, примерно, бракованных изделий (назовем это число M) в партии из 10000 единиц ?) p = 0.8; M = 800 ?) p = 0.92; M = 800 ?) p = 0.7; M = 700 ?) p = 0.08; M = 100 Вопрос id:1606278 Для построения доверительного интервала для оценки вероятности надо пользоваться таблицами ?) распределения Стьюдента ?) нормального распределения ?) распределения Пирсона ( 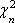 ) )?) распределения Стьюдента или распределения Пирсона ( 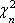 ) )Вопрос id:1606279 Для проверки на всхожесть было посеяно 2000 семян, из которых 1700 проросло. Определите вероятность p прорастания отдельного семени в этой партии и количество семян в среднем (назовем это число M), которое взойдет из каждой тысячи посеянных ?) p=0.15; M=150 ?) q=3/20; M=800 ?) p=17/20; M=750 ?) p=0.85; M=850 Вопрос id:1606280 Если вероятность р некоторого события неизвестна, а для оценки этой вероятности производится n испытаний, то 95%-ый доверительный интервал для величины р находится по формуле ?) I0,95 (p)= 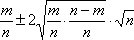 ?) I0,95 (p)= 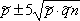 , где , где  ?) I0,95 (p)=  , где , где  ?) I0,95 (p)=  Вопрос id:1606281 Если вероятность события A есть р(, то найдите вероятность события, ему противоположного ?) 1-р( ?) 1 ?) 0 ?) 0.5 Вопрос id:1606282 Если имеется группа из n несовместных событий Hi, в сумме составляющих все пространство, и известны вероятности P(Hi), а событие A может наступить после реализации одного из Hi и известны вероятности P(A/Hi), то P( вычисляется по формуле ?) Байеса ?) Муавра-Лапласа ?) Полной вероятности ?) Бернулли Вопрос id:1606283 Завод в среднем дает 27% продукции высшего сорта и 70% - первого сорта. Найдите вероятность того, что наудачу взятое изделие не будет высшего или первого сорта ?) 0.03 ?) 0.27 ?) 0.7 ?) 0.97 Вопрос id:1606284 Завод в среднем дает 28% продукции высшего сорта и 70% - первого сорта. Найдите вероятность того, что наудачу взятое изделие будет или высшего, или первого сорта ?) 0.97 ?) 0.7 ?) 0.02 ?) 0.98 Вопрос id:1606285 Задана таблица распределения случайной величины. Найти C 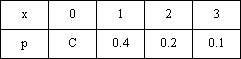 ?) 0.3 ?) 0.5 ?) 0.2 ?) 0.4 Вопрос id:1606286 Задана таблица распределения случайной величины. Найти р(X < 3) 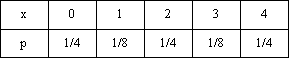 ?) 5/8 ?) 3/8 ?) 1/2 ?) 3/4 Вопрос id:1606287 Из колоды, состоящей из 36 карт, вынимают наугад две карты. Вероятность того, что попадут две карты одинаковой масти равна ?) 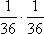 ?) 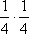 ?) 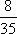 ?) 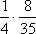 Вопрос id:1606288 Из колоды, состоящей из 36 карт, вынимают наугад две карты. Вероятность того, что это будут две пики равна ?) 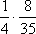 ?) 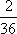 ?) 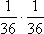 ?) 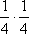 Вопрос id:1606289 Изделия изготавливаются независимо друг от друга. В среднем одно изделие из ста оказывается бракованным. Найдите вероятность того, что из 200 взятых наугад изделий 2 окажутся неисправными ?) 0.01 ?) 0.024 ?) 0.271 ?) 0.001 Вопрос id:1606290 Изделия изготавливаются независимо друг от друга. В среднем одно изделие из ста оказывается бракованным. Найдите вероятность того, что из двух взятых наугад изделий окажутся неисправными оба ?) 0.001 ?) 0.01 ?) 0.0001 ?) 0.02 Вопрос id:1606291 Имеется группа из n несовместных событий Hi, в сумме составляющих все пространство, и известны вероятности P(Hi), а событие A может наступить после реализации одного из Hi, и заданы вероятности P(A/Hi). Известно, событие A произошло. Вероятность, что при этом была реализована Hi вычисляется по формуле ?) Муавра-Лапласа ?) Байеса ?) Полной вероятности ?) Бернулли Вопрос id:1606292 Количество поражений шахматиста в течение года имеет распределение Пуассона с параметром λ=6. Вероятность того, что шахматист в течение года проиграет не более двух партий равна ?) 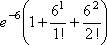 ?) 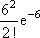 ?) 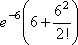 ?) 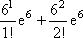 Вопрос id:1606293 Количество Х принимаемых по телефону за час звонков имеет распределение Пуассона. Среднее количество принимаемых за час звонков λ=5. Вероятность того, что за час будет принято точно 3 звонка равна ?) 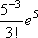 ?) 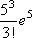 ?) 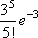 ?) 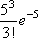 Вопрос id:1606294 Куплено 1000 лотерейных билетов. На 80 из них упал выигрыш по 1 руб., на 20 - по 5 руб., на 10 - по 10 руб. Найдите таблицу, описывающую закон распределения выигрыша ?) 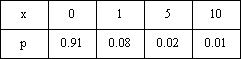 ?) 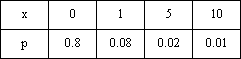 ?) 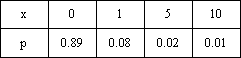 ?) 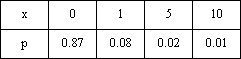 Вопрос id:1606295 Куплено 500 лотерейных билетов. На 40 из них упал выигрыш по 1 руб., на 10 - по 5 руб., на 5 - по 10 руб. Найдите средний выигрыш, приходящийся на один билет ?) 0.28 ?) 2 ?) 0.35 ?) 1
|
Copyright testserver.pro 2013-2024