Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийЗадачи и методы оптимизации (для аспирантов, курс 1)Вопрос id:1588004 Необходимым условием экстремума функционала является ?) Обращение в ноль 1-й и 2-й вариаций функционала ?) Обращение в ноль 2-й вариации функционала ?) Обращение в ноль 1-й вариации функционала ?) Положительность 1-й и 2-й вариаций функционала Вопрос id:1588005 Общий вид уравнения Эйлера следующий ?) 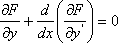 ?) 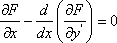 ?) 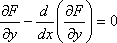 ?) 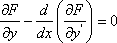 Вопрос id:1588006 Оптимизацию можно определить как ?) определение целевого функционала ?) свойство сложных систем управления ?) процесс нахождения наилучшего решения задачи по некоторому критерию ?) выбор некоторого критерия оптимизации из нескольких возможных Вопрос id:1588007 Первые четыре числа ряда Фибоначчи равны 1, 1, 2, 3. Пятое число ряда равно ?) 7 ?) 6 ?) 4 ?) 5 Вопрос id:1588008 Переход от исходной прямоугольной системы координат к косоугольной в симплекс-методе производится введением ?) дополнительных не основных ограничений ?) специальных связанных переменных ?) специальных параметров ?) дополнительных не основных свободных переменных Вопрос id:1588009 Переход от исходной прямоугольной системы координат к косоугольной в симплекс-методе производится введением ?) специальных параметров ?) дополнительных ограничений ?) дополнительных свободных переменных ?) специальных связанных переменных Вопрос id:1588010 Постановка задачи оптимизации предполагает наличие ?) оптимизирующей процедуры ?) объекта оптимизации и цели оптимизации ?) системы оптимальных процедур ?) метода расчета критерия оптимизации Вопрос id:1588011 Прагматические критерии оптимизации - это ?) критерии, получаемые на основе решения уравнения Эйлера ?) критерии, полученные на основе математических расчетов ?) выработанные практикой количественные характеристики оптимальности некоторой системы ?) специальные критерии, используемые при расчетах строительных конструкций Вопрос id:1588012 При равенстве нулю 1-й вариации функционала данный функционал достигает на кривой максимума, если 2-я вариация функционала ?) больше максимального значения функции ?) меньше, чем 1-я вариация функционала ?) меньше нуля ?) больше нуля Вопрос id:1588013 При равенстве нулю 1-й вариации функционала функционал достигает на кривой минимума, если 2-я вариация функционала ?) больше, чем 1-я вариация функционала ?) меньше нуля ?) больше нуля ?) меньше минимального значения функции Вопрос id:1588014 Примером функционала может служить выражение ?)  ?)  ?)  ?)  Вопрос id:1588015 Примером функционала может является ?) множество ?) предел последовательности ?) дифференциал ?) определенный интеграл от функции Вопрос id:1588016 Примером функционала может являться ?) алгебраическое уравнение ?) дифференциал функции ?) сопоставление каждой функции ее максимального значения на отрезке ?) вариация функции Вопрос id:1588017 Принцип Гамильтона в классической механике формулируется так ?) система движется между двумя точками в фазовом пространстве по кратчайшей траектории ?) система движется между двумя точками в фазовом пространстве так, чтобы время движения было минимальным ?) система движется между двумя точками в фазовом пространстве по такой траектории, для которой некоторый интегральный функционал, называемый действием, сохраняет постоянное значение ?) система движется между двумя точками в фазовом пространстве по такой траектории, для которой некоторый интегральный функционал, называемый действием, обращается в минимум Вопрос id:1588018 Принцип оптимальности Беллмана можно сформулировать так: оптимальная траектория ?) состоит из частей-траекторий, начальная и конечная из которых оптимизируется собственным функционалом для соответствующей конечной и начальной точки ?) состоит из частей-траекторий, каждая из которых оптимизируется собственным функционалом для соответствующей конечной и начальной точки ?) является единой траекторией, оптимизируемой соответствующим функционалом ?) состоит из частей-траекторий, каждая из которых не является оптимальной Вопрос id:1588019 Пусть задан функционал I(y(x)+eh(x)) (e-число), тогда 1-й вариацией функционала является выражение ?)  ?)  ?)  ?)  Вопрос id:1588020 Пусть задан функционал I(y(x)+eh(x)) (e-число), тогда 2-й вариацией функционала является выражение ?)  ?)  ?)  ?)  Вопрос id:1588021 Решение задач линейного программирования дает ?) один экстремум ?) не более трех экстремумов ?) два или более экстремума ?) не более двух экстремумов Вопрос id:1588022 Решение задач нелинейного программирования может давать в общем случае ?) два или более экстремума ?) не более трех экстремумов ?) только один экстремум ?) не более двух экстремумов Вопрос id:1588023 Решения задачи линейного программирования - это ?) минимум линейной формы ?) минимакс линейной формы ?) значения n переменных xj ?) максимум линейной формы Вопрос id:1588024 Симплекс-метод в линейном программировании - это метод ?) модификации ограничений ?) оптимального (направленного) перебора ?) нахождения нулей линейной формы ?) покоординатного спуска Вопрос id:1588025 Симплекс-метод обеспечивает сходимость к экстремальной точке за ___ число шагов ?) нечетное ?) четное ?) бесконечное ?) конечное Вопрос id:1588026 Теорема Куна - Таккера в выпуклом программировании обобщает ?) теорему Лагранжа для классических задач ?) методы динамического программирования ?) градиентные методы ?) симплекс-метод Вопрос id:1588027 Теоретически нелинейное программирование разработано только для ___ функций ?) кусочно-гладких ?) интегрируемых ?) выпуклых ?) разрывных Вопрос id:1588028 Уравнение Эйлера для функционала  имеет вид?)  ?)  ?)  ?) 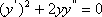 Вопрос id:1588029 Уравнения Гамильтона представляют собой систему ?) двух дифференциальных уравнений 1-го порядка ?) двух дифференциальных уравнений 2-го порядка ?) двух алгебраических уравнений ?) трех дифференциальных уравнений 1-го порядка Вопрос id:1588030 Функция f(x,y) 2-х переменных называется выпуклой функцией в выпуклой области G, если для любых двух точек из G выполняется соотношение при 0≤l≤1 ?) 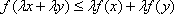 ?) 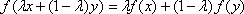 ?) 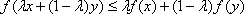 ?) 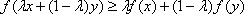 Вопрос id:1588031 Функция f(x,y) 2-х переменных называется сепарабельной, если она представлена в виде ?) 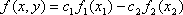 ?) 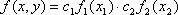 ?) 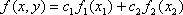 ?)  Вопрос id:1588032 Число ограничений - n и число переменных - m в задачах нелинейного программирования удовлетворяют условию ?) n и m могут быть любыми ?) m=n ?) n>m ?) m<n Вопрос id:1588033 Число частей, на которые делится отрезок в методе дихотомии равно ?) 3 ?) 2 ?) 4 ?) 5 Вопрос id:1588034 Экстремум в задачах линейного программирования ?) двойственный ?) единственный, т. е. локальный и глобальный одновременно ?) множественный ?) только локальный Вопрос id:1588035 Экстремумы линейных форм прямой и двойственной задач линейного программирования ?) не совпадают ?) совпадают по модулю ?) обратные друг к другу ?) совпадают Вопрос id:1588036 Алгоритм называется полиномиальным, если время его работы T(n) ограничено сверху некоторым полиномом ?) да ?) нет Вопрос id:1588037 Алгоритм называется экспоненциальным, если время его работы T(n) ограничено снизу некоторым полиномом ?) да ?) нет Вопрос id:1588038 В задачах целочисленного программирования переменные задачи могут принимать только целые значения ?) да ?) нет Вопрос id:1588039 В задаче коммивояжера ищется максимум целевой функции ?) да ?) нет Вопрос id:1588040 В задаче о камнях веса камней входят в целевую функцию ?) да ?) нет Вопрос id:1588041 В задаче о рюкзаке его грузоподъемность V входит в целевую функцию ?) да ?) нет Вопрос id:1588042 В основе комбинаторных методов лежит идея разбиения области допустимых решений ?) да ?) нет Вопрос id:1588043 В худшем случае метод ветвей и границ сводится к полному перебору всех возможных вариантов решения задачи ?) нет ?) да Вопрос id:1588044 Задача коммивояжера принадлежит классу NP задач ?) да ?) нет Вопрос id:1588045 Задача называется полностью целочисленной, если условие целочисленности наложено на все ее переменные ?) нет ?) да Вопрос id:1588046 Задача с ослабленными ограничениями - задача, которая возникает в результате исключения требования целочисленности некоторых переменных ?) да ?) нет Вопрос id:1588047 Задача с ослабленными ограничениями - задача, которая возникает в результате исключения требования целочисленности переменных ?) нет ?) да Вопрос id:1588048 Класс Р состоит из задач, для которых существуют полиномиальные алгоритмы решения ?) да ?) нет Вопрос id:1588049 Комбинаторные методы используются, если число переменных велико ?) нет ?) да Вопрос id:1588050 Любая задача с конечным множеством допустимых решений может быть решена методом перебора ?) да ?) нет Вопрос id:1588051 Метод ветвей и границ применяется в задачах, где число допустимых решений конечно ?) да ?) нет Вопрос id:1588052 Рекуррентное соотношение Беллмана используется в методе ветвей и границ ?) да ?) нет Вопрос id:1588053 В задачах выпуклого программирования целевая функция и допустимая область решений являются выпуклыми множествами ?) нет ?) да |
Copyright testserver.pro 2013-2024