|
|
Список вопросов базы знанийМатематический анализ (курс 5)Вопрос id:781740 Установите соответствие между профессиональными терминами и их определениями | Левая часть | Правая часть | Правило Лопиталя | прямая L называется асимптотой кривой, если расстояние от точки на кривой до L стремится к нулю, когда точка неограниченно удаляется от начала координат | Асимптоты кривой | представление функции, имеющей в окрестности 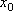 производные до ( n+1) порядка, в виде суммы многочлена степени n, расположенного по степеням 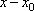 и некоторого остаточного члена, содержащего 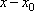 в ( n+1) степени | Вертикальная асимптота графика | если 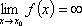 , то прямая 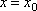 – вертикальная асимптота графика y= f( x) | Формула Тейлора | служит для нахождения 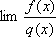 , когда 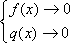 (неопределенность  ), или 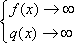 (неопределенность  ); правило утверждает: если существует предел (конечный или бесконечный) отношения производных  , то существует и предел функций 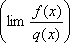 и эти пределы равны | Наклонная асимптота графика | прямая y= kx+ b – наклонная асимптота (в частности, при k = 0 – горизонтальная), если 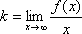 , 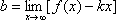 , при нахождении наклонных асимптот надо различать случаи 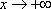 и 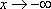 |
Вопрос id:781786 Длина дуги кривой 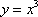 с концами в точках О(0, 0) и А(3, 27) вычисляется с помощью интеграла Вопрос id:781787 Длина дуги параболы 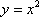 с концами в точках О(0, 0) и А(2, 4) вычисляется с помощью интеграла Вопрос id:781794 Для интегралов 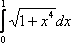 и 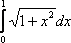 на основании свойства монотонности интеграла имеет место неравенство Вопрос id:781800 Для функции 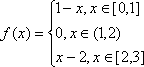 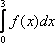 равен Вопрос id:781803 Интеграл 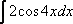 равен Вопрос id:781913 Интеграл  равен Вопрос id:781915 Интеграл 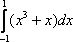 равен Вопрос id:781916 Интеграл 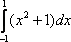 равен ?) 4 ?)  ?) 0 ?)  Вопрос id:781917 Интеграл 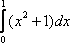 равен ?) 2 ?) 1 ?)  ?)  Вопрос id:781919 Интеграл 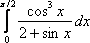 заменой переменной 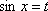 сводится к интегралу Вопрос id:781925 Интеграл 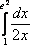 равен ?) 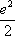 ?)  ?) 1 ?) 2 Вопрос id:781926 Интеграл 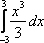 равен Вопрос id:781928 Интеграл 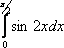 равен Вопрос id:781930 Интеграл 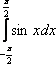 равен Вопрос id:781931 Интеграл 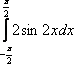 равен Вопрос id:781932 Интеграл 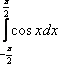 равен Вопрос id:781934 Несобственный интеграл 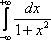 ?) расходится ?) равен  ?) равен 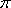 ?) равен 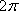 Вопрос id:781936 Несобственный интеграл 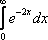 ?) равен -2 ?) равен  ?) расходится ?) равен 2 Вопрос id:781938 Несобственный интеграл 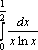 ?) равен 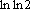 ?) расходится ?) равен 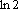 ?) равен 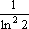 Вопрос id:781940 Объем тела, образованного вращением вокруг оси 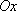 фигуры, ограниченной линиями 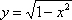 и 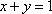 , равен разности интегралов Вопрос id:781941 Объем тела, образованного вращением вокруг оси 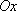 фигуры, ограниченной параболой 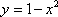 и осью 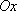 , вычисляется с помощью интеграла Вопрос id:781943 Определенным интегралом 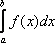 называется предел Вопрос id:781949 Площадь криволинейного треугольника, ограниченного гиперболой 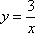 и прямыми 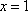 и 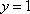 , равна Вопрос id:781952 Площадь криволинейной трапеции 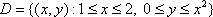 равна Вопрос id:781954 Площадь криволинейной трапеции 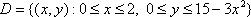 равна Вопрос id:781955 Площадь криволинейной трапеции 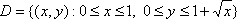 равна Вопрос id:781957 Площадь области, ограниченной линиями 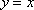 и 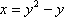 , вычисляется с помощью определенного интеграла Вопрос id:781961 Площадь параболического сегмента, ограниченного параболой 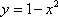 и осью 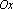 , равна Вопрос id:781963 Разложение дроби 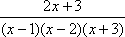 на простейшие равно Вопрос id:781965 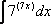 равен Вопрос id:781974 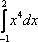 равен Вопрос id:781975 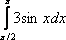 равен Вопрос id:781976 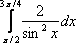 равен Вопрос id:785782 Установите соответствие между профессиональными терминами и их определениями | Левая часть | Правая часть | Действительные числа | числа, которые представляются бесконечными непериодическими десятичными дробями | Элементы множества | совокупность, набор каких-то предметов | Рациональные числа | целые числа или обыкновенные дроби, т.е. отношение целых чисел | Иррациональные числа | предметы, составляющие множество | Множество | положительные и отрицательные рациональные и иррациональные числа, число нуль | Пустое множество | множество, не содержащее ни одного элемента |
Вопрос id:785783 Установите соответствие между профессиональными терминами и их определениями | Левая часть | Правая часть | Окрестность точки 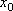 | число А называют пределом числовой последовательности 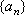 , если для любого как угодно малого положительного числа 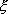 существует номер N такой, что все члены последовательности 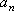 c номерами 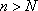 удовлетворяют неравенству 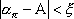 | Переменная величина | Величина, принимающая различные значения | Числовая последовательность | открытый интервал с центром в точке 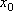 длиной 2 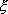 , т.е. 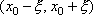 | Область значений переменной величины | Множество всех значений, которые принимает (пробегает) данная переменная величина | Предел числовой последовательности | любой открытый интервал, содержащий эту точку | 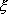 – окрестность точки 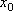 |  задана, если каждому натуральному числу n по некоторому закону поставлено в соответствие определенное действительное число 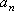 |
Вопрос id:785784 Установите соответствие между профессиональными терминами и их определениями | Левая часть | Правая часть | Единственность предела последовательности | если она является либо неубывающей, либо невозрастающей | Сходящаяся и расходящаяся последовательность | последовательность, имеющая (конечный) предел, и последовательность, не имеющая предела | Монотонная последовательность | если существует число 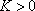 такое, что для любого n выполнено равенство 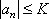 | Бесконечно большая последовательность | последовательность 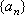 не может иметь двух различных пределов | Необходимое и достаточное условие сходимости последовательности  | если для любого как угодно большого числа M > 0 существует N такой, что 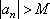 , 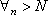 | Ограниченная последовательность 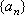 | для любого 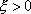 существовал N такой, что для всех  выполнялось неравенство 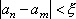 |
Вопрос id:785785 Установите соответствие между профессиональными терминами и их определениями | Левая часть | Правая часть | Сложная функция (функция от функции) и ее производная | если задана функция y=f(x), то x называется независимой переменной, или аргументом | Область значений функции | y= f( u), где u= φ( x), т.е. y= f[ φ( x)] – сложная функция, 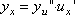 | Обратная функция и ее дифференцирование | множество значений, принимаемых функций | График функции y=f(x) | если y= f( x) разрешить относительно x: x= φ( y), то φ( y) – обратная функция к f( x). Производные обратных функций являются взаимно обратными величинами: 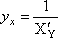 | Параметрическое задание функции. Дифференцирование параметрических заданных уравнений | множество точек на плоскости, абсциссами которых являются значения аргумента, а ординатами значения функции, соответствующие этим значениям аргумента; множество точек (x ; f(x)) | Независимая переменная, аргумент | переменная величина y есть функция переменной x, если каждому значению x по некоторому правилу поставлено в соответствие определенное значение y; запись y=f(x) | Область определения функции | множество (область) значений аргумента | Функция | связь между аргументом x и функцией y выражена через посредство третьей переменной t-параметра; x и y заданы как функции параметра: x= φ( t), 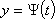 производная: 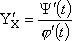 |
Вопрос id:785786 Установите соответствие между профессиональными терминами и их определениями | Левая часть | Правая часть | Бесконечно большая (б.б.) | переменная величина х называется бесконечно большой, если обратная величина 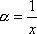 – бесконечно малая | Сравнение бесконечно малых (б.м.) | переменная величина  называется бесконечно малой, если она стремится к нулю (число 0 – ее предел):  | Предел переменной величины х | число а есть предел переменной величины х, если для любого 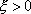 , начиная с некоторого момента в изменении х, выполняется неравенство  ; запись lim x = a или если 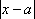 абсолютная величина разности между х и а становится в процессе изменения переменной величины х сколь угодно малой | Бесконечно малая (б.м.) |  , если для 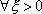 найдется такое 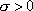 , что для х, лежащего в  – окрестности 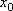 и 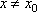 , выполняется неравенство 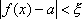 , или 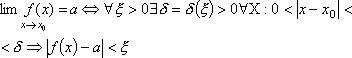 | Предел функции f( x) в точке 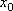 (при 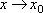 ) | найти предел отношения двух бесконечно малых α и β 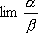 : если 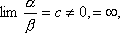 то α и β – одного порядка; в частности, если 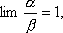 то α и β – эквивалентные б.м.; если 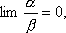 α – высшего порядка (малости) по сравнению с β; запись α =0(β) | Предел функции при 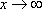 | 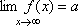 , если для 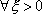 найдется такое N, что 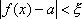 при 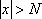 |
Вопрос id:785787 Установите соответствие между профессиональными терминами и их определениями | Левая часть | Правая часть | Касательная прямая | 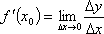 – предел отношения приращения функции к приращению аргумента в точке 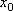 , когда приращение аргумента стремится к нулю | Физические интерпретации производной | 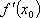 – скорость изменения функции y= f( x) в точке  (относительно изменения аргумента x); если S= f( t) зависимость пути от времени, то 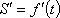 (производная пути по времени) – скорость движения в момент t | Производная функции y= f( x)в точке 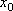 | предельное положение секущей, когда две точки ее пересечения с линией стремятся слиться в одну | Геометрический смысл производной | 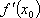 – тангенс угла наклона касательной к графику функции y= f( x), проведенной в точке 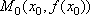 | Непрерывность функции в точке 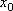 | функция y= f( x) непрерывна в точке 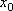 , если  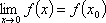 ; другое определение: пусть 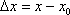 (приращение аргумента) и 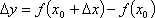 (приращение функции) тогда функция непрерывна в точке 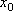 , если б.м. приращению 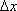 соответствует б.м. приращение функции 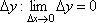 |
Вопрос id:785788 Установите соответствие между профессиональными терминами и их определениями | Левая часть | Правая часть | Дифференцируемая функция | дифференциал 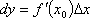 – приращение ординаты касательной прямой, проведенной к графику функции y= f( x) в точке 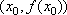 | Дифференциал функции y=f(x) | функция y= f( x) дифференцируема в точке 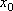 , если существует (конечная) производная 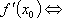 существует дифференциал 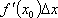 ; дифференцируемая в 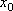 функция непрерывна в 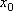 , обратное неверно | Инвариантность формы записи дифференциала | тоже, произвольное приращение независимой переменной 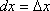 | Дифференциал независимой переменной | форма записи дифференциала функции 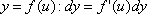 не зависит от того, будет ли u независимым или промежуточным аргументом | Геометрический смысл дифференциала функции y=f(x) | дифференциал dy есть главная часть приращения функции, пропорциональная приращению аргумента 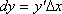 ; 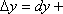 б.м. высшего порядка относительно 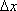 |
Вопрос id:785789 Установите соответствие между профессиональными терминами и их определениями | Левая часть | Правая часть | Теорема о хорде и касательной | если 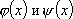 непрерывны [ a, b] и дифференцированы на ( a, b), причем 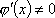 на ( a, b), то 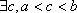 : 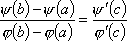 | Теорема Коши | специальный случай теоремы о хорде и касательной для графика функции y= f( x) на [ a, b]: существует точка с, a < c < b такая, что 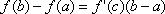 | Теорема Ролля | если у кривой линии в каждой ее точке существует касательная, то найдется точка, в которой касательная параллельна хорде | Теорема (формула) Лагранжа | специальный случай теоремы Лагранжа: если f( a)= f( b), то  ; теоремы Лагранжа и Ролля верны для функции f( x), непрерывной на [ a, b] и дифференцируемой по крайней мере на ( a, b) |
Вопрос id:785790 Установите соответствие между профессиональными терминами и их определениями | Левая часть | Правая часть | Точки максимума, минимума, экстремума |  – выпукла, 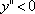 – вогнута | Точка перегиба | 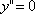 или не существует – необходимый признак, 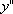 меняет знак при переходе через точку 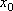 , тогда в точке 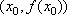 – перегиб – достаточный признак | Признак возрастания или убывания | если производная при переходе слева направо через 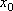 , где выполняется необходимое условие экстремума меняет знак с + на – , то х 0 – точка максимума, если с – на +, 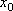 – точка минимума | Достаточный признак экстремума | точка на кривой, которая отделяет участок выпуклости от участка вогнутости | Монотонные функции (возрастающая и убывающая) | кривая выпукла (вогнута), если лежит над (под) любой своей касательной | Признак выпуклости (вогнутости) | 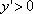 – функция возрастает, 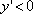 – функция убывает | Выпуклость (вогнутость) кривой | точка 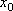 – точка максимума (минимума) функции f( x), если значение 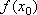 больше (меньше) всех значений f( x), принимаемых в некоторой окрестности 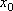 ; определение подчеркивает локальный характер понятия; точка экстремума – общее назначение точек максимума и минимума | Признаки точки перегиба | функция возрастает (убывает), если большему значению аргумента соответствует большее (меньшее) значение функции |
|
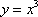 с концами в точках О(0, 0) и А(3, 27) вычисляется с помощью интеграла
с концами в точках О(0, 0) и А(3, 27) вычисляется с помощью интеграла



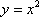 с концами в точках О(0, 0) и А(2, 4) вычисляется с помощью интеграла
с концами в точках О(0, 0) и А(2, 4) вычисляется с помощью интеграла



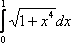 и
и 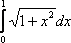 на основании свойства монотонности интеграла имеет место неравенство
на основании свойства монотонности интеграла имеет место неравенство



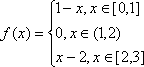
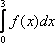 равен
равен



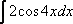 равен
равен



 равен
равен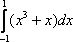 равен
равен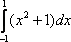 равен
равен

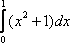 равен
равен

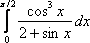 заменой переменной
заменой переменной 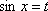 сводится к интегралу
сводится к интегралу



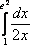 равен
равен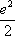

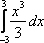 равен
равен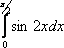 равен
равен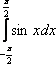 равен
равен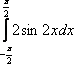 равен
равен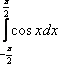 равен
равен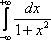

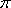
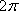
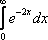

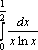
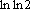
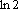
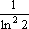
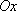 фигуры, ограниченной линиями
фигуры, ограниченной линиями 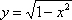 и
и 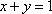 , равен разности интегралов
, равен разности интегралов



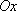 фигуры, ограниченной параболой
фигуры, ограниченной параболой 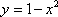 и осью
и осью 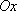 , вычисляется с помощью интеграла
, вычисляется с помощью интеграла



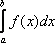 называется предел
называется предел , где
, где  ,
,  ,
, 
 , где
, где  ,
,  ,
, 
 , где
, где  ,
,  ,
, 
 , где
, где  ,
,  ,
, 
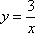 и прямыми
и прямыми 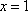 и
и 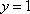 , равна
, равна



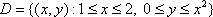 равна
равна



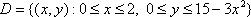 равна
равна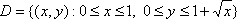 равна
равна


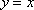 и
и 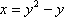 , вычисляется с помощью определенного интеграла
, вычисляется с помощью определенного интеграла



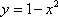 и осью
и осью 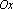 , равна
, равна



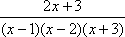 на простейшие равно
на простейшие равно



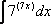 равен
равен



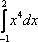 равен
равен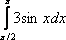 равен
равен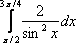 равен
равен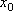 производные до (n+1) порядка, в виде суммы многочлена степени n, расположенного по степеням
производные до (n+1) порядка, в виде суммы многочлена степени n, расположенного по степеням 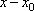 и некоторого остаточного члена, содержащего
и некоторого остаточного члена, содержащего 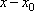 в (n+1) степени
в (n+1) степени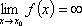 , то прямая
, то прямая 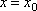 – вертикальная асимптота графика y=f(x)
– вертикальная асимптота графика y=f(x)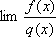 , когда
, когда 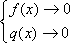 (неопределенность
(неопределенность  ), или
), или 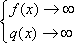 (неопределенность
(неопределенность  ); правило утверждает: если существует предел (конечный или бесконечный) отношения производных
); правило утверждает: если существует предел (конечный или бесконечный) отношения производных  , то существует и предел функций
, то существует и предел функций 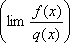 и эти пределы равны
и эти пределы равны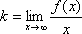 ,
, 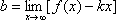 , при нахождении наклонных асимптот надо различать случаи
, при нахождении наклонных асимптот надо различать случаи 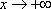 и
и 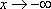
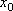
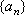 , если для любого как угодно малого положительного числа
, если для любого как угодно малого положительного числа 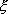 существует номер N такой, что все члены последовательности
существует номер N такой, что все члены последовательности 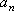 c номерами
c номерами 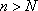 удовлетворяют неравенству
удовлетворяют неравенству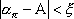
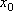 длиной 2
длиной 2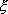 , т.е.
, т.е. 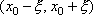
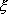 – окрестность точки
– окрестность точки 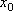
 задана, если каждому натуральному числу n по некоторому закону поставлено в соответствие определенное действительное число
задана, если каждому натуральному числу n по некоторому закону поставлено в соответствие определенное действительное число 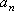
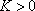 такое, что для любого n выполнено равенство
такое, что для любого n выполнено равенство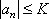
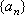 не может иметь двух различных пределов
не может иметь двух различных пределов
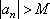 ,
, 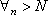
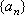
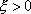 существовал N такой, что для всех
существовал N такой, что для всех  выполнялось неравенство
выполнялось неравенство 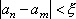
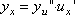
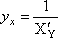
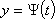 производная:
производная: 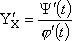
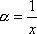 – бесконечно малая
– бесконечно малая называется бесконечно малой, если она стремится к нулю (число 0 – ее предел):
называется бесконечно малой, если она стремится к нулю (число 0 – ее предел): 
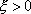 , начиная с некоторого момента в изменении х, выполняется неравенство
, начиная с некоторого момента в изменении х, выполняется неравенство  ; запись limx = a или если
; запись limx = a или если 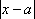 абсолютная величина разности между х и а становится в процессе изменения переменной величины х сколь угодно малой
абсолютная величина разности между х и а становится в процессе изменения переменной величины х сколь угодно малой , если для
, если для 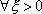 найдется такое
найдется такое 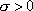 , что для х, лежащего в
, что для х, лежащего в  – окрестности
– окрестности 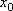 и
и 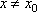 , выполняется неравенство
, выполняется неравенство 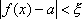 , или
, или 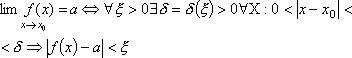
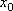 (при
(при 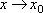 )
)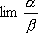 : если
: если 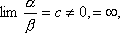 то α и β – одного порядка; в частности, если
то α и β – одного порядка; в частности, если 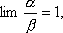 то α и β – эквивалентные б.м.; если
то α и β – эквивалентные б.м.; если 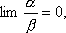 α – высшего порядка (малости) по сравнению с β; запись α =0(β)
α – высшего порядка (малости) по сравнению с β; запись α =0(β)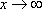
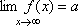 , если для
, если для 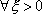 найдется такое N, что
найдется такое N, что 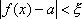 при
при 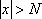
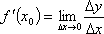 – предел отношения приращения функции к приращению аргумента в точке
– предел отношения приращения функции к приращению аргумента в точке 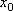 , когда приращение аргумента стремится к нулю
, когда приращение аргумента стремится к нулю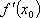 – скорость изменения функции y=f(x) в точке
– скорость изменения функции y=f(x) в точке  (относительно изменения аргумента x); если S=f(t) зависимость пути от времени, то
(относительно изменения аргумента x); если S=f(t) зависимость пути от времени, то 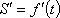 (производная пути по времени) – скорость движения в момент t
(производная пути по времени) – скорость движения в момент t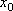
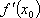 – тангенс угла наклона касательной к графику функции y=f(x), проведенной в точке
– тангенс угла наклона касательной к графику функции y=f(x), проведенной в точке 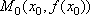
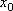
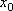 , если
, если 
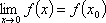 ; другое определение: пусть
; другое определение: пусть 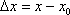 (приращение аргумента) и
(приращение аргумента) и 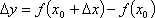 (приращение функции) тогда функция непрерывна в точке
(приращение функции) тогда функция непрерывна в точке 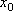 , если б.м. приращению
, если б.м. приращению 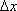 соответствует б.м. приращение функции
соответствует б.м. приращение функции 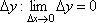
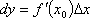 – приращение ординаты касательной прямой, проведенной к графику функции y=f(x) в точке
– приращение ординаты касательной прямой, проведенной к графику функции y=f(x) в точке 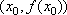
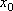 , если существует (конечная) производная
, если существует (конечная) производная 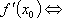 существует дифференциал
существует дифференциал 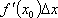 ; дифференцируемая в
; дифференцируемая в 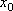 функция непрерывна в
функция непрерывна в 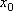 , обратное неверно
, обратное неверно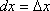
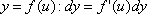 не зависит от того, будет ли u независимым или промежуточным аргументом
не зависит от того, будет ли u независимым или промежуточным аргументом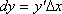 ;
; 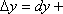 б.м. высшего порядка относительно
б.м. высшего порядка относительно 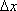
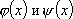 непрерывны [a,b] и дифференцированы на (a,b), причем
непрерывны [a,b] и дифференцированы на (a,b), причем 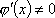 на (a,b), то
на (a,b), то 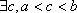 :
: 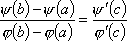
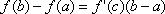
 ; теоремы Лагранжа и Ролля верны для функции f(x), непрерывной на [a,b] и дифференцируемой по крайней мере на (a,b)
; теоремы Лагранжа и Ролля верны для функции f(x), непрерывной на [a,b] и дифференцируемой по крайней мере на (a,b) – выпукла,
– выпукла, 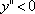 – вогнута
– вогнута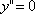 или не существует – необходимый признак,
или не существует – необходимый признак, 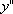 меняет знак при переходе через точку
меняет знак при переходе через точку 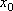 , тогда в точке
, тогда в точке 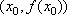 – перегиб – достаточный признак
– перегиб – достаточный признак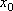 , где выполняется необходимое условие экстремума меняет знак с + на – , то х0 – точка максимума, если с – на +,
, где выполняется необходимое условие экстремума меняет знак с + на – , то х0 – точка максимума, если с – на +, 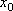 – точка минимума
– точка минимума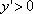 – функция возрастает,
– функция возрастает, 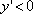 – функция убывает
– функция убывает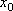 – точка максимума (минимума) функции f(x), если значение
– точка максимума (минимума) функции f(x), если значение 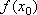 больше (меньше) всех значений f(x), принимаемых в некоторой окрестности
больше (меньше) всех значений f(x), принимаемых в некоторой окрестности 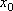 ; определение подчеркивает локальный характер понятия; точка экстремума – общее назначение точек максимума и минимума
; определение подчеркивает локальный характер понятия; точка экстремума – общее назначение точек максимума и минимума